
你能区分数学和诗歌吗?参加测验找出答案
“_______是逻辑思想的______”—阿尔伯特·爱因斯坦。 “数学”或“诗歌”这两个词填空哪个更合适?
伊芙琳·兰姆是一位居住在犹他州盐湖城的自由数学和科学作家。

你能区分数学和诗歌吗?参加测验找出答案
“_______是逻辑思想的______”—阿尔伯特·爱因斯坦。 “数学”或“诗歌”这两个词填空哪个更合适?

我最喜欢的空间之几:圆环面
数学总是与可定向的亏格为 1 的糕点搭配更佳,这是最美味的拓扑学例子。

跑步中的数学
如果你以每公里 3:07 的平均速度跑完一场比赛,你是否在任何一公里都正好跑了 3:07?嗯,这很复杂。

解开变形空间的奥秘,数学家赢得 300 万美元奖金
第二届年度数学突破奖授予加州大学伯克利分校的拓扑学家伊恩·阿戈尔
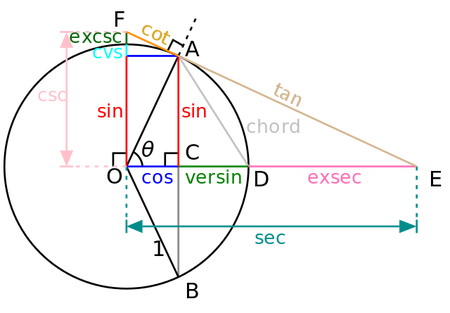
我写过的最可怕的数学故事
读完这些后,你可能需要在晚上开着灯睡觉。准备好迎接僵尸、恶魔、木乃伊和……更高阶的同伦群了吗?

争议教学:5 × 3 是五个 3 还是三个 5?
最新的(被误称的)“共同核心数学”争议:5 × 3 是五个 3 还是三个 5?
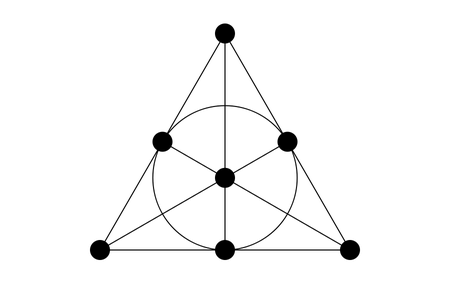
我最喜欢的空间之几:法诺平面
挑战直觉的法诺平面可能是点和线最小的有趣配置。

ε 和 δ 的诡计
ε-δ 证明是许多微积分学生的克星,是进入证明写作奥秘的入门仪式。

一次一刀,制作你自己的字体
四色定理靠边站!现在是单刀定理的时间了:如果你愿意进行一些巧妙的折叠,你可以用一刀剪出任何你想要的形状
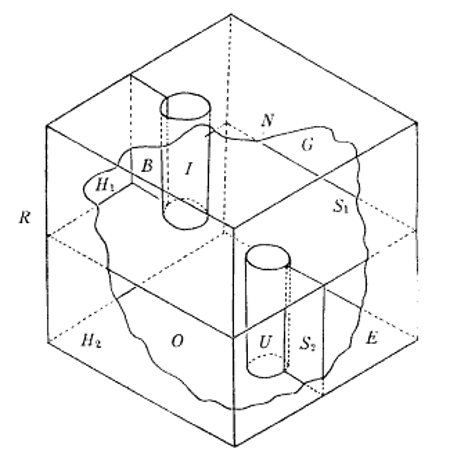
我最喜欢的空间之几:双室房屋
理解一个数学对象意味着什么?在我为自己建造双室房屋之前,我并没有真正相信它的存在。

不可能的壁纸和神秘曲线:探索数学和艺术中的对称性
在他的新书《创造对称性》中,弗兰克·法里斯运用高等数学的思想,如复分析和抽象代数,将风景、鲜花,甚至他的晚餐快照转化为美丽的重复设计。
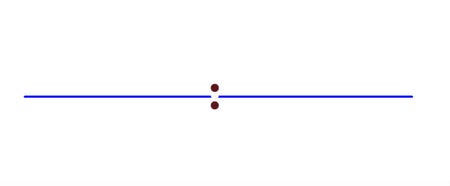
我最喜欢的空间之几:具有两个原点的直线
这条可证明不可绘制的具有两个原点的直线说明了一个简单但重要的拓扑性质

改变你的开集,改变你的人生
开集的概念是拓扑学的基础。它是什么,为什么它很重要?

在 8,812 孔甜甜圈上的史诗般的探索
大卫·马多尔的在线迷宫让你可以在你最喜欢的网络浏览器的舒适环境中探索复杂的双曲曲面。

在双曲平面中一切看起来都更好
将你自己或你最喜欢的数学家变成双曲平面的平铺艺术品。
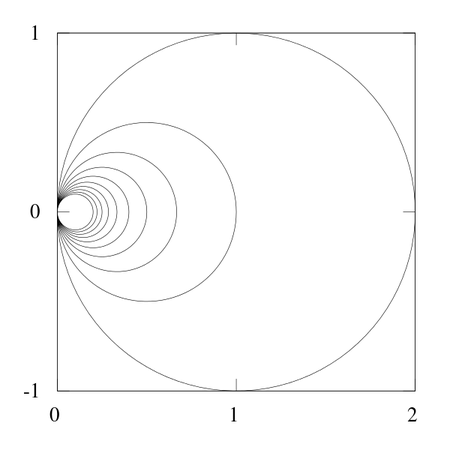
我最喜欢的空间之几:无限耳环
拓扑学是关于挤压和拉伸的;距离应该无关紧要。但是无限耳环说明了拓扑学和几何学之间微妙的相互作用。
在 Bridges 与我一起制作数学音乐
加入我在巴尔的摩 Bridges 数学+艺术会议上的数学、音律和音高感知研讨会。

世界上最准确的镶木地板性格测试
你是神经质的孤独者还是有魅力的邪教领袖?试试这个高度科学的性格测试,它基于安东尼·高迪的现代主义杰作之一的镶木地板来找出答案

成为塞德里克·维拉尼是什么感觉
菲尔兹奖章获得者的回忆录让我们得以一窥成为一位充满热情的数学家的情感高潮和低谷。

帮助让可穿戴蜂窝自动机成为现实
法比安·塞里耶想要破解一台工业针织机来制作蜂窝自动机围巾,你可以在 Kickstarter 上支持她的项目。

作为数学家难以忍受的字面主义
数学家,就像盗窃癖患者一样,会字面意思地理解事物。这是一个关于我如何最终爆发并写了一篇措辞强烈的博文,解释了为什么文学免责声明让我恼火的故事。

对莫扎特和模算术的迟来的道歉
莫扎特和模算术有什么共同之处?我曾经认为我不喜欢它们。对不起,莫扎特和模算术。请原谅我。
我最喜欢的空间之几:康托的漏帐篷
称为康托的漏帐篷的数学空间是连通的,但仅仅是勉强连通:移除一个点,整个结构就会瓦解。

当《蒙娜丽莎》是 NP 困难问题时
鲍勃·博世和汤姆·韦克斯勒开发了一种新方法,可以将你最喜欢的杰作变成连点成线谜题。你只需要一点量化和大量的计算时间。