法国数学家爱德华·卢卡斯于 1842 年出生于亚眠,49 年后在巴黎去世。他撰写了四卷本著作《数学娱乐》,该书成为休闲数学的经典之作。1883 年,他以笔名“N. 克劳斯·德·暹罗”(“卢卡斯·德·亚眠”的 anagram)推销了一种单人游戏,他称之为河内塔。
他声称这款游戏是所谓梵天塔的简化版。在这一假想的传说中,僧侣们必须在一个宏伟的寺庙中移动一座由 64 个金盘组成的塔。然而,在他们完成这项任务之前,寺庙就会化为尘土,世界末日就会到来。
河内塔由一个小型木板组成,木板上安装了三个相同的圆柱形杆。左杆上有五个大小不同的圆盘,中间有一个孔。它们按大小排列,最大的圆盘在底部。游戏的目标是以尽可能少的步数将所有圆盘从左杆移动到右杆。在每一步中,只能从一根杆上取出一个圆盘并将其放置在另一根杆上,并且永远不能将较大的圆盘放在较小的圆盘上。运输这些圆盘需要多少步,以及哪些步骤是必要的?
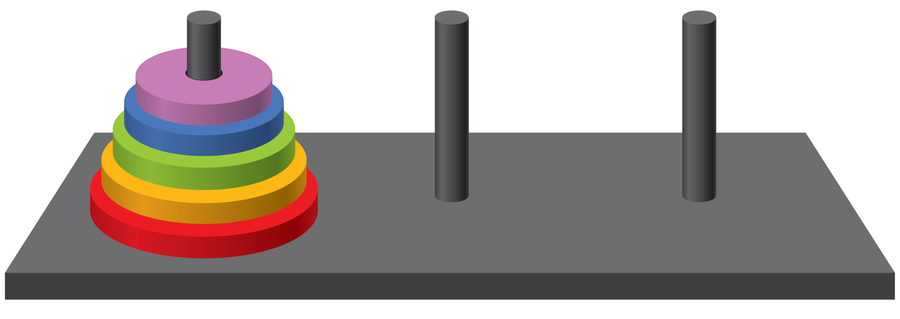
阿曼达·蒙塔内斯
我们根据大小用数字替换圆盘。现在我们系统地构建解决方案,从只有一个圆盘的塔开始。解决方案很简单。只需一步,您就可以将单个圆盘从左边移动到右边。

阿曼达·蒙塔内斯
对于有两个圆盘的塔,您首先将圆盘 1 从左边移动到中间,然后将圆盘 2 从左边移动到右边,最后将圆盘 1 从中间移动到右边。因此,您需要 3 = 22 – 1 步。
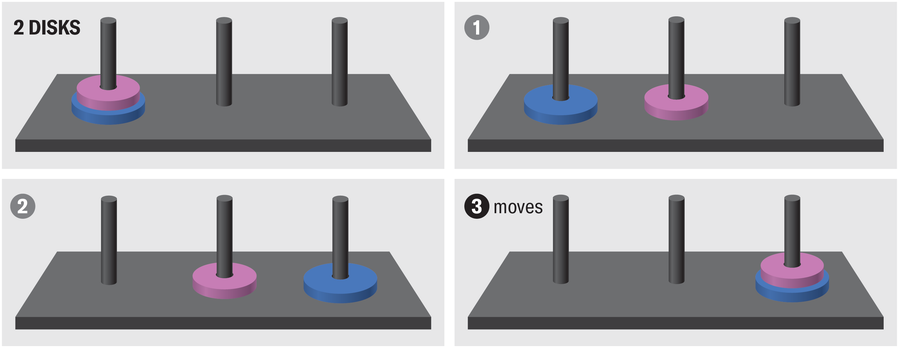
阿曼达·蒙塔内斯
对于有三个圆盘的塔,我们首先在脑海中忽略圆盘 3。这会将问题简化为只有两个圆盘的任务,我们现在用三步将其从左边移动到中间。在第四步中,我们将圆盘 3 从左边移动到右边。现在我们再次在脑海中忽略圆盘 3,再次用三步将两个圆盘从中间移动到右边。总共需要 3 + 1 + 3 = 7 = 23 – 1 步。

阿曼达·蒙塔内斯
对于四个圆盘的塔的问题,可以用非常类似的方式简化为三个圆盘的塔的问题。因此,您需要 7 + 1 + 7 = 15 = 24 – 1 步。最后,对于五个圆盘的塔,您需要 15 + 1 + 15 = 31 = 25 – 1 步。一般来说,对于有 n 个圆盘的塔,您需要 2n – 1 步。爱德华·卢卡斯最初的游戏有八个圆盘。
我们很乐意听到您的来信!请发送电子邮件至 games@sciam.com 分享您的体验。
这个谜题最初出现在《Spektrum der Wissenschaft》中,并经许可转载。