本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定代表《大众科学》的观点
艾伦·图灵在《形态发生的化学基础》中提出,化学物质(形态素)可以转化并在组织中扩散,从而产生在动物身上看到的自然图案——条纹、斑点和螺旋。图灵用微分方程的语言表达了这个想法,微分方程的初始条件控制着图案的演变。
这种反应-扩散系统产生的图案的复杂性和细节可能非常令人惊讶——一个相对简单的过程和少量的参数可以产生无穷无尽的熟悉图案和形状。一个应季的例子是雪花,以其多样性和复杂性而闻名。
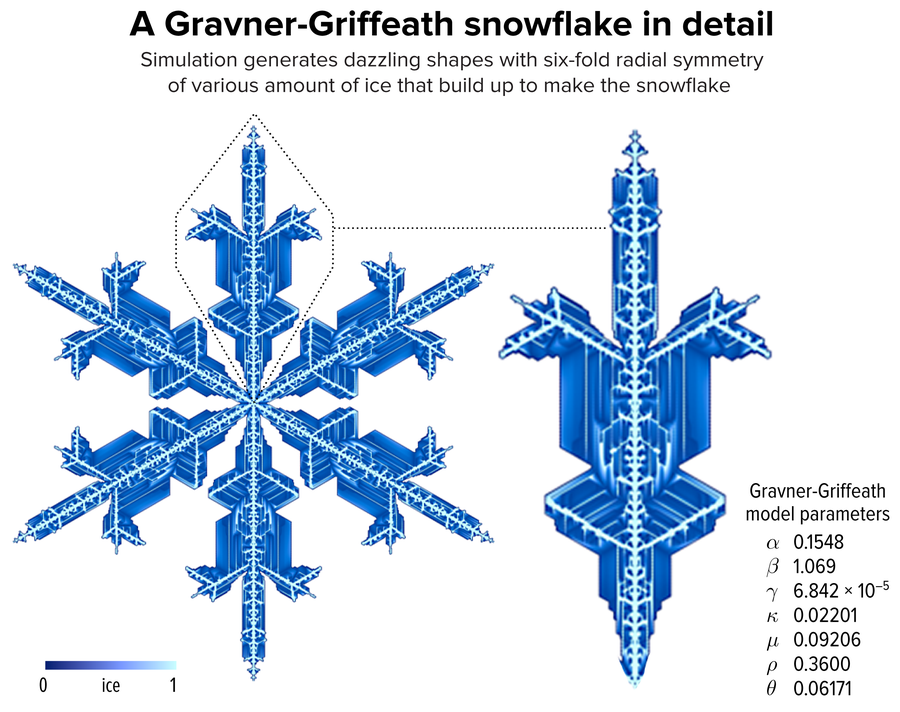
图 1. 使用 Gravner-Griffeath 模型生长的雪花示例。雪花不同部位的不同冰量(用蓝色调编码)构成了六重径向对称形状。您可以在我们的在线雪花收藏中浏览有关此雪花的详细信息。致谢:Martin Krzywinski 和 Jake Lever
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
使用 Gravner-Griffeath 模型可以模拟出令人信服的逼真雪花,您可以使用作者提供的代码自行运行(图 2)。雪花的径向对称性继承自它生长的六边形网格。在不同的网格站点模拟了三种不同类型的质量:冰、准液体和蒸汽。最初,在雪花站点初始化 ρ 量的冰,并在其他所有地方初始化 ρ 蒸汽质量。然后,该模型通过扩散、冻结(由 κ 控制)和融化(由 μ 和 γ 控制)来传输和转换这些质量的一部分。例如,在冻结过程中,边界质量处一部分 κ 的蒸汽变成冰,剩余部分 1–κ 变成准液体。雪花周围的边界站点通过附着过程成为雪花的一部分,该过程由参数 α、β 和 θ 控制,这些参数充当截止值。一旦一个站点成为雪花的一部分,它的所有质量都变成不再变化的冰。

图 2. Gravner-Griffeath 模型是一种反应-扩散系统,具有三种“形态素”:冰、准液体和蒸汽。该模型是确定性的——给定一组参数,输出始终相同。可选地,该模型可以通过在每个步骤扰动每个站点中的蒸汽质量量来包含随机性。致谢:Martin Krzywinski 和 Jake Lever
我们所有的雪花都在 800 × 800 的六边形网格上生长,最多 30,000 个生长步骤,并在此处以矩形网格呈现,通过旋转和缩放获得。雪花始终以网格中心的单个站点初始化,当它们生长到接近网格边界时,被认为已完全长大,此时模拟结束。在图 3 中,我们跟踪了图 1 中雪花的生长过程。选择颜色图是为了在浅色背景上绘制时突出雪花的边界——请注意,浅蓝色代表高质量,而深蓝色代表低质量。

图 3. 雪花从图 1 到完全长大(15,353 个生长步骤)的演变过程。致谢:Martin Krzywinski 和 Jake Lever
图 1 中的雪花用了 15,353 步才完全长大。在图 3 的第一行图像中可以看到生长速度。在第二行中,每张图像都被放大不同的量,以更好地揭示较小雪花生长过程的细节。请记住,一旦一个站点加入雪花,其质量在模拟期间是固定的。最初,冰质量沿着对称轴累积,并迅速开始出现微小的凸起。这些凸起长成树枝,因为蒸汽不必像到达雪花其他部分那样扩散那么远才能到达凸起。这个过程称为分支不稳定性,并产生树枝状雪花。
雪花在内角处生长迅速,因为对于拥有超过 3 个雪花邻居的边界站点,附着过程是自动的。这使得沉积物具有少量质量(深蓝色)来填充雪花。这称为刻面,它与分支相反。刻面雪花具有简单的平坦表面。到 2,000 次迭代时,我们看到分支减慢,并且出现越来越多的刻面(深蓝色)。
蒸汽的作用可以在第三行图像中看到,该图像使用灰度描绘了每个空气站点中的蒸汽质量量。蒸汽量通过冻结 (κ)、融化 (γ) 以及附着影响冰的形成,其中如果其邻域中的蒸汽量小于 θ 且准液体量高于 α,则具有三个雪花邻居的边界单元可以附着。

图 4. 改变每个模型参数对图 1 中雪花形状的影响,其参数值显示为红点。图像对小黑刻度线显示的参数值进行采样。我们的雪花集合中按参数值分布的情况显示为灰色直方图。中位数是箱子之间的长黑线。致谢:Martin Krzywinski 和 Jake Lever
尽管该模型相对简单,但参数对雪花形状的影响却相当复杂。为了了解参数如何影响形状,我们使用图 1 中的雪花作为对照,并在可行雪花的范围内系统地改变了它的每个参数。我们所说的“可行”是指那些在 30,000 次迭代后没有长成微不足道的六边形并且占据了六边形网格 60% 以上的雪花——这类雪花约占使用随机生成的参数值生长的雪花的 10%。
例如,增加控制总质量量的 ρ 会提高生长速度并鼓励分支。我们图 1 中的雪花 ρ 值较低,因此分支不多。增加 θ 和减少 α 都会鼓励刻面,因为这些参数是附着的截止值。
鉴于图 4 中形状的巨大变化,尝试根据相似性对雪花进行聚类是合理的。已经有人提出了复杂的雪花分类系统。这些包括扇形板(简单六边形,图 4 中 θ = 0.081)、星状板(完全星状雪花,图 4 中 μ = 0.072)、星状枝晶(分支雪花,图 4 中 α = 0.18)和蕨状星状枝晶(高度分支,图 4 中 ρ = 0.5)等类别。有趣的是,通过改变图 1 中雪花(星状枝晶)的单个参数,可以用多种方式获得这些类别中的每一个。
对雪花进行分组有两种选择:按参数值或按形状。最初,我们的计划是按参数创建分组,我们认为这更接近模型的内部工作原理。然而,如图 4 所示,参数空间非常混乱——参数的微小变化可能会导致形状的巨大差异。因此,我们选择使用形状,我们希望这将创建更具视觉吸引力的组,我们稍后可以将这些组与参数值相关联(图 5)。
由于我们在 800 × 800 的网格上生长雪花,因此每片雪花都可以被视为长度为 640,000 的向量,其中的值是蒸汽或冰质量。具有相似向量(通过欧几里得距离测量)的雪花具有相似的形状。但是,对于我们大约 15,000 片雪花的集合,对如此大的向量进行聚类在计算上是不可行的。我们通过将雪花按五分之一的因子进行下采样来解决这个问题,以创建一个 160 × 160 的网格,我们进一步使用高斯滤波器对其进行模糊处理,以消除相似雪花之间的小差异。任何一对雪花之间的相似性是相应 25,600 元素向量之间的欧几里得距离。
使用计算出的雪花之间的相似性,我们对它们的“距离”有了一个概念。不幸的是,这个距离是在一个 25,600 维的空间中表示的。为了可视化这个空间,习惯上将这个空间降维到二维,以便我们可以在页面上绘制它。
对此的常用方法是主成分分析 (PCA),它识别数据集内最大方差的轴,并旋转数据,使第一维显示最大方差。本质上,选择旋转是为了尽可能多地保留数据中的趋势。PCA 假设数据集具有线性,这当然被我们的雪花所违反。然而,PCA 识别出 θ(附着)和 ρ(质量)与前两个主成分高度相关。这确实按雪花的“丰满度”对雪花进行了分离,但无法区分较小的分组。
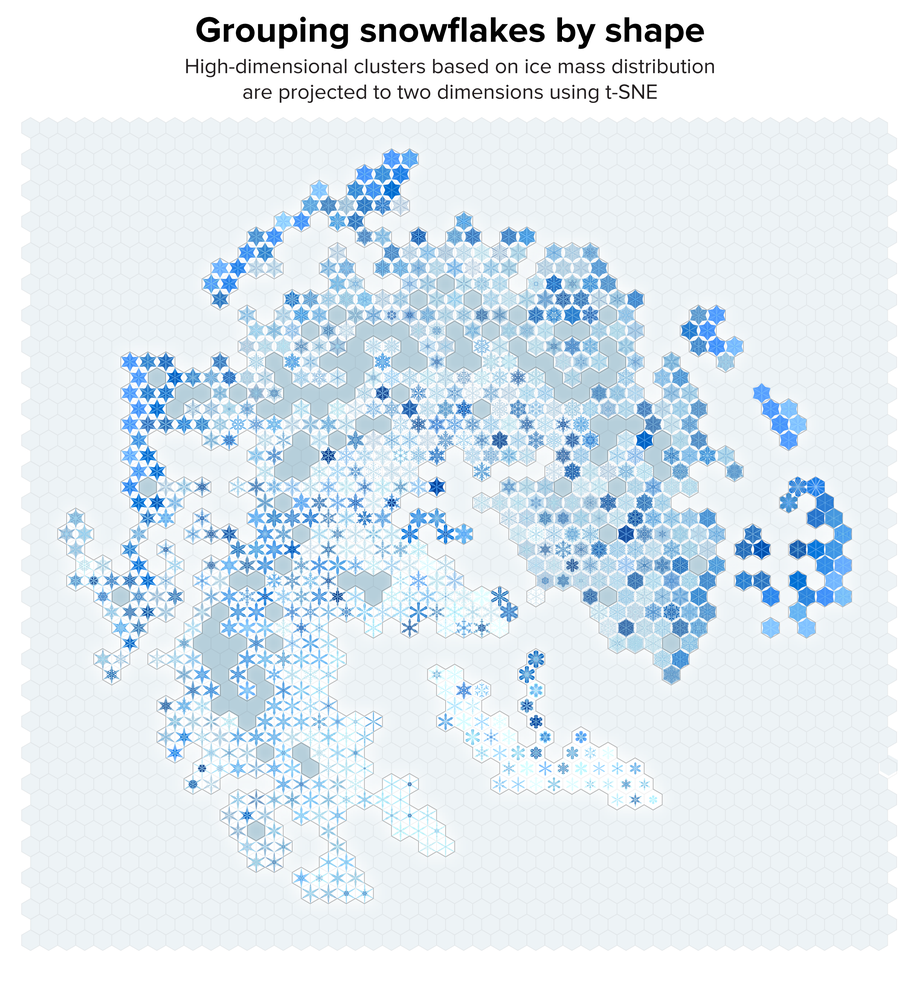
图 5. 我们基于结构相似性聚类的雪花集合。使用 t-SNE 将聚类投影到二维空间。雪花本身排列在六边形网格上,以实现更紧密的堆积。致谢:Martin Krzywinski 和 Jake Lever
PCA 的替代方法是 t-分布随机邻域嵌入 (t-SNE)。此方法使用以下原理:高维空间中相似的雪花应放置在低维空间中彼此靠近的位置。它将两片雪花的相似性建模为高维空间和低维空间中的概率分布,并最大限度地减少这两个分布之间的差异。设 dij 为雪花 i 和 j 之间的欧几里得距离,则
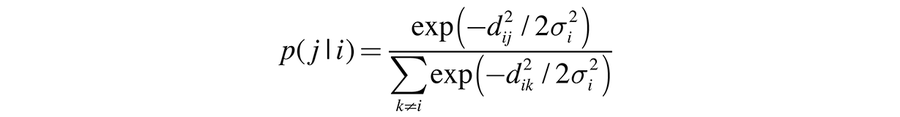
是选择雪花 j 作为雪花 i 的邻居的条件概率。
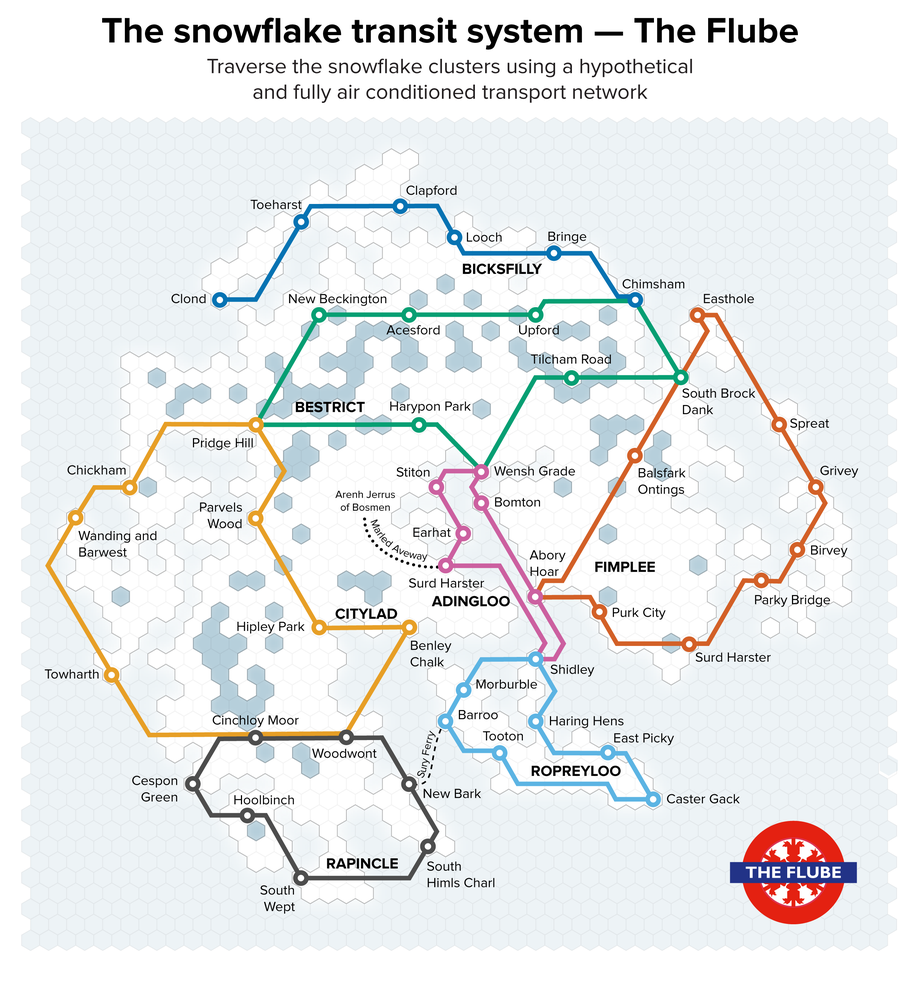
图 6. 雪花二维 t-SNE 空间中的路径集合,昵称为“The Flube”。致谢:Martin Krzywinski 和 Jake Lever
我们已经使用 t-SNE 构建了一个雪花世界——一种通常有助于具体说明聚类之间关系的可视化过程——我们想到扩展这片想象中的土地,使其拥有自己的交通系统,该系统将在这个大陆上形成一个网络,使雪花能够在各个区域之间通行。自然而然地,我们将这个系统命名为“The Flube”(图 6)。
由于雪花是模拟的,我们还使用在 622 个伦敦地铁和铁路站名称上训练的循环神经网络 (RNN) 模拟了 The Flube 中线路和车站的名称。我们根据名称的感知个性将名称分组到线路中:Ropreyloo 充满趣味性,车站如 East Picky 和 Morburble;Citylad 很时髦,车站如 Benley Chalk 和 Wanding & Barwest;而 Bicksfilly 沿线的 Bringe 和 Clapford 等车站不太可能是受欢迎的旅游目的地。
RNN 是马尔可夫模型的更复杂版本,马尔可夫模型是一种有限状态自动机,可以根据从字母(或单词)训练集中学习到的特定概率生成字母(或单词)。转移的概率仅基于机器的当前状态,而不使用所有先前的输出。另一方面,RNN 将传统神经网络与内部状态相结合。此状态跟踪网络的所有先前输入,因此会记住生成单词中的先前字母。RNN 概念已用于生成类似莎士比亚的英语、食谱和说唱歌词。
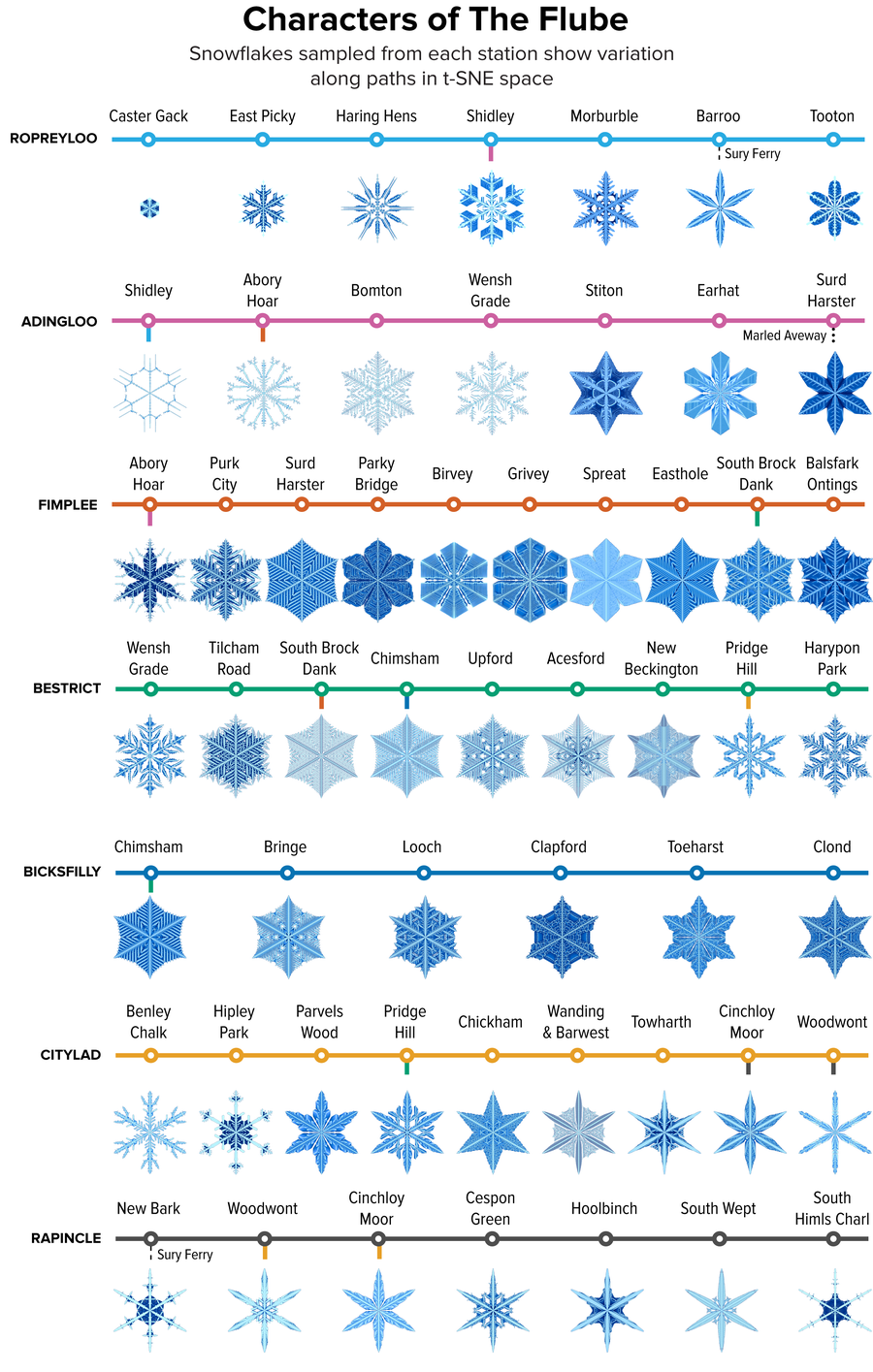
图 7. The Flube 中每个车站的 t-SNE 六边形网格中发现的雪花样本,显示了聚类内部和聚类之间的形状变化。致谢:Martin Krzywinski 和 Jake Lever
我们可以使用 Flube 线路和车站来采样 t-SNE 空间(图 7),就像图 2 中显示的参数空间采样一样。我们根据我们对雪花形状的印象分配了线路和车站名称。较小(年轻)的雪花被分配了有趣的 Ropreyloo 线路,而北部的雪花,我们认为那里是偏远而严酷的土地,则获得了 Bicksfilly。从 Caster Gack 到 Clond 的路程很长(需要四次换乘:Shindley、Abory Hoar、South Brock Dank 和 Chimsham)。
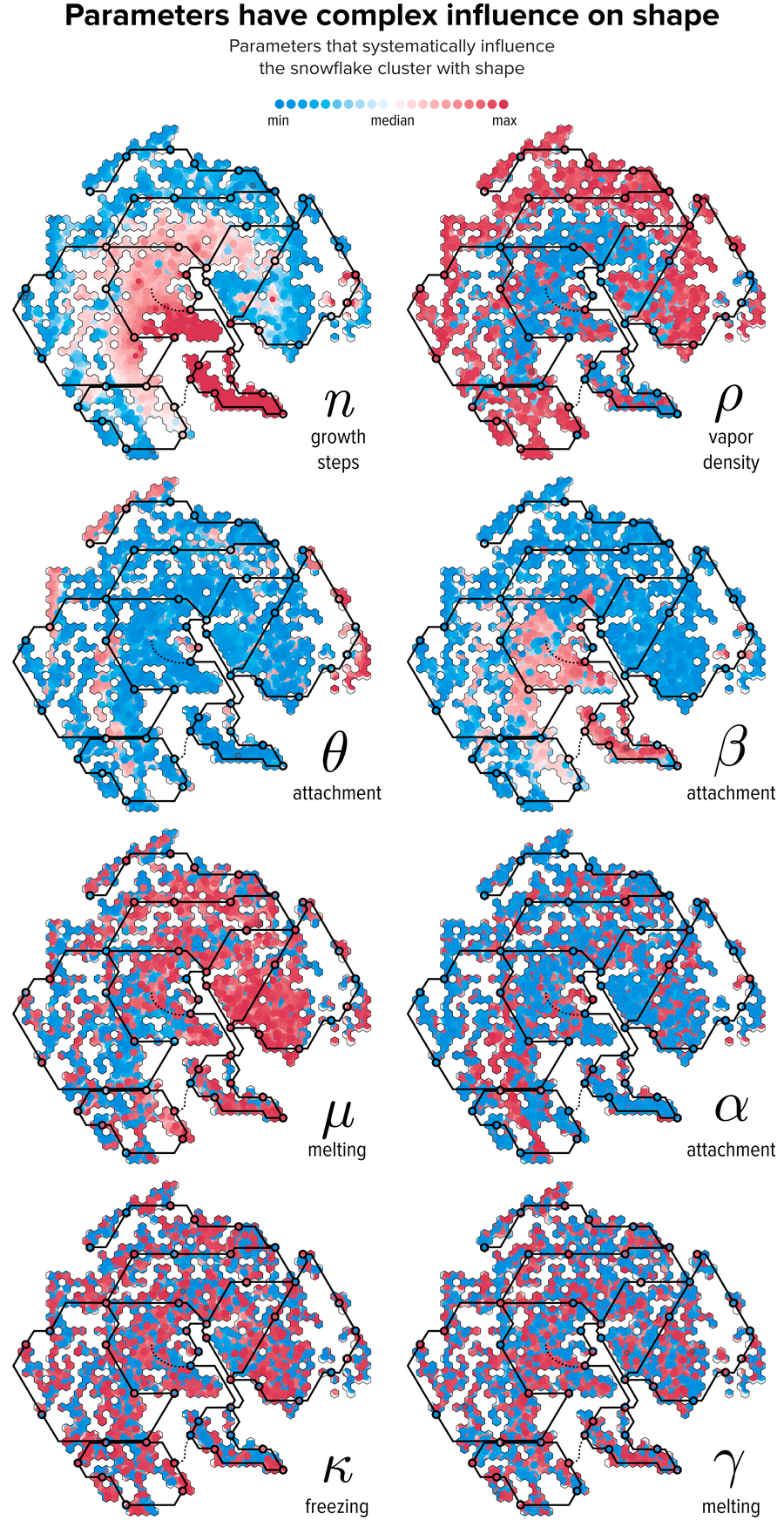
图 8. 参数值与 t-SNE 聚类之间的关系。每片雪花都绘制成一个圆圈,颜色由雪花参数与中位值的相对差异决定。叠加了 The Flube 的线路,以帮助解释图 7 中的形状变化。致谢:Martin Krzywinski 和 Jake Lever
图 8 将参数值与 t-SNE 聚类联系起来。t-SNE 大陆上的雪花形状现在可以通过其参数来解释。例如,南部(Ropreyloo)带有小雪花的岛屿对应于低 θ 和低 ρ,高 α 和高 β。北部半岛(Bicksfilly)和东部岛屿群(Fimplee)带有星状板雪花(高 θ)。陆地中心(Bestrict)主要由蕨状枝晶(低 ρ)组成,而西南次大陆(Rapincle)有许多星状枝晶(低 α)。
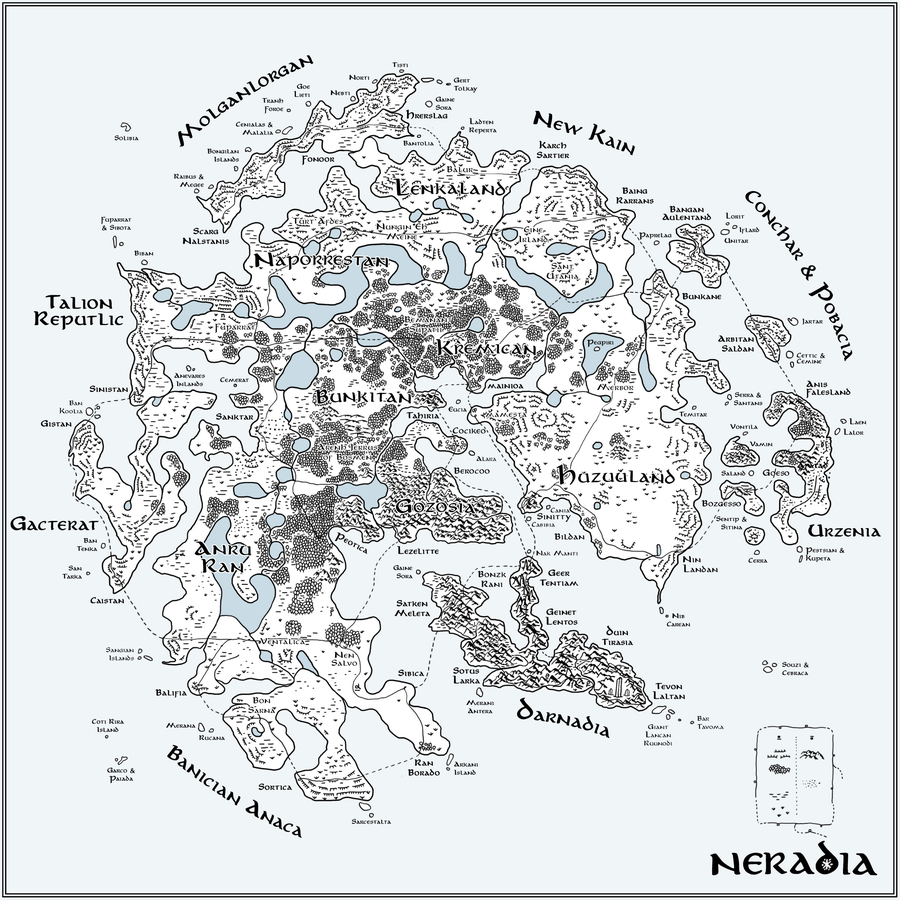
图 9. 图 5 中 t-SNE 地图的手绘解释。地理特征编码参数值:森林(低 ρ)、草原(低 β)、沼泽(低 μ)和沙漠(高 θ)。雪花生长的速度(达到完全大小的步数,n)由山脉(高 n)和冰崖(低 n)编码。所有名称均使用在 257 个国家/地区名称上训练的 RNN 生成。Flube 网络绘制为细线,车站为环路,城市(中等大小文本)放置在图 6 中车站位置的位置。致谢:Martin Krzywinski 和 Jake Lever
一旦我们创建了交通系统,下一步就是想象一个完整的世界,我们称之为 Neradia。通过将参数值编码为地理特征并使用在 257 个国家/地区名称上训练的 RNN,我们生成了图 9 中 t-SNE 地图的手绘版本,风格类似于托尔金。
即使使用像 257 个国家/地区名称这样的小型训练集,RNN 输出也非常有趣。我们最喜欢的是 Conchar & Pobacia(东北)和 New Kain(北部)地区。The Flube 中每个车站的位置都分配了一个城市名称,以保持车站名称的风格。Clapford 车站位于 Molganlorgan 地区的 Hrerslag 市,Abory Hoar 位于 Huzuuland 地区的 Sinnity 市。RNN 对字母的奇怪失误,例如将“islands”变为“inlands”,出现在“Anevares Inlands”中,后者是 Talion Reputlic 地区深处的一组岛屿(一个滑稽的拼写错误)。
我们已经在一个名为“unwords”的集合中探索了使用 RNN 生成其他文本。你的朋友劝阻你不要将你的第一个女儿命名为 Ginavietta Xilly Anganelel,但你没有听。当你将你的第二个女儿命名为 Nabule Yama Janda 时,每个人都想知道你拥有如此成功的孩子的秘诀是什么。男孩也有很多选择:Babton Laarco Tabrit 和 Ferandulde Hommanloco Kictortick。让我们希望没有人患有 myconomascophobia,永远不会被 cakmiran 咬伤,并渴望成为 gabdologists。
图 1 中的示例雪花被分配了来自 Bosmen 的 Arenh Jerrus 的 RNN 输出,并根据其在 Bunkitan 地区森林中的 t-SNE 位置绘制在地图上。这片雪花在 The Flube 地图上足够重要,拥有其专用连接线,称为 Marled Aweway,它起源于 Adingloo 线路上的 Surd Harster。
下次当您身处暴风雪中或辛勤地铲雪时,请向 Neradia 的居民问好,并思考一个关于您自己数据的故事。
我们要感谢 Lisa Shiozaki 和 Rodrigo Goya 的有益讨论。本文中包含的图像的高分辨率版本可以在 Krzywinski 的网站上查看。
