本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
对于犹他州人来说,欣赏户外风光几乎是合同规定的。我的德克萨斯州血统至今阻止我成为一名滑雪者——徒步旅行更符合我的节奏。徒步旅行给了我很多:锻炼、新鲜空气、野生动物和有趣的岩石景观,偶尔还能让我对某个数学问题产生新的看法。最近一次徒步旅行中,我和我的配偶高估了我们的耐力,低估了我们选择的 trail 的难度,我对芝诺悖论有了更深刻、更发自内心的理解。
大约2500年前,埃利亚的芝诺提出了一些相关的悖论,讨论运动是否是一种幻觉。我在徒步旅行中思考的那个悖论有时被称为二分法悖论,当人们在谈话中提到芝诺悖论时,这可能是大多数人想到的那个。它是这样的:为了从 A 点到达 B 点,你必须首先跨越 A 点到 B 点距离的一半,然后跨越剩余距离的一半,然后再跨越从该点开始的剩余距离的一半,依此类推。你永远无法到达目的地,因为你必须在旅途中访问无数个中间点。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
深入探讨这个论点,即使是为了到达中点,我们仍然有另一个芝诺悖论需要克服。我们必须到达中点的一半,以及该点的一半。这种推理似乎暗示运动是不可能的。然而,我们的生活和我们的徒步旅行证明了我们确实可以从 A 点到达 B 点。
对于刚入门的数学家来说,这个悖论通常是他们最初接触无穷概念并与我们有限的人类在试图理解它时遇到的内在矛盾作斗争的地方。但是,尽管芝诺悖论很流行,但它对我来说从来没有真正产生过冲击。当我第一次遇到它时,我太务实了——显然我可以走过房间,所以我们为什么要担心这个呢?它对我来说总是显得有点傻。直到那次徒步旅行。
那次徒步旅行是我们两天内的第二次艰难徒步。我的小腿肌肉又紧又酸痛。我的脚上好几处都起了水泡,每走一步都变得更加疼痛。我的背包带和汗湿的衬衫摩擦着我的肩膀和臀部。在我们所在的高度,海拔超过 10,000 英尺,每一次呼吸都感觉不足,每一步都是来之不易的胜利。最重要的是,我有点想小便了。
我开始痴迷地查看徒步旅行应用程序上的 GPS。每次查看时,我都会进行一些心算。到山顶还有多远?当我们掉头后,我还剩下多远的路程?在我回到 trail head,享受堆肥厕所和汽车舒适座椅带来的幸福解脱之前,我必须先走到一半的路程。那是在过溪流之前还是之后?一旦我们到达中点,我们就必须走完返回 trail head 的剩余距离的一半,并到达危险的陡峭之字形路段。一旦我们到达那里,我们仍然需要到达 trail head 距离的一半。就在那时,我们看到了两只驼鹿——一只母鹿和它看起来笨拙,但仍然巨大而有力的幼崽——当我们默默地站在 trail 旁边,等待动物们吃饱并离开时,悖论似乎更加真实了。
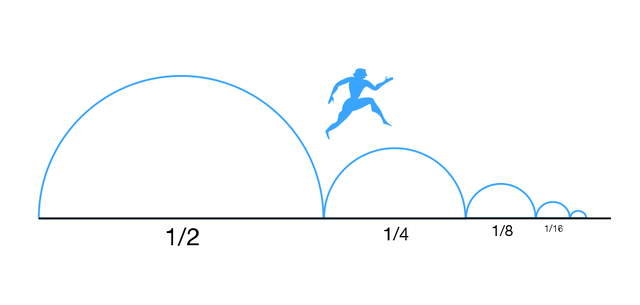
从数学角度解释和解决芝诺悖论并不太难。亚里士多德指出,随着距离的减小,所需的时间也会减少。今天,我们可以使他的论点更加精确,写下无穷级数的和,有时甚至从中得到一个有限的数字。在芝诺悖论的情况下,我们可以将这种情况表示为 1/2+1/4+1/8+1/16+… 的和,它加起来等于数字 1。因此,如果我们以恒定的速度移动,或者即使我们感到疲倦但仍以快于某个最小速度的速度继续前进,我们最终将跨越两个地点之间的距离。
在 trail 上,解决芝诺悖论不是一个总结漂亮的几何级数的问题。而是在于不顾水泡、摩擦、稀薄的空气以及在舒适的岩石上休息片刻的诱惑,大胆地一只脚接一只脚地向前迈进。
有关芝诺悖论的更多信息,请查看 BBC 广播节目《In Our Time》的最新一集,或查看 Vi Hart 关于微积分和人行横道的有趣视频。有关另一位“山上的芝诺”,请查看我的数学上的哥哥 Zeno Huang,他也喜欢在美国西部各州徒步旅行。
