本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
今年早些时候,玛丽娜·维亚佐夫斯卡展示了如何在八维空间中最有效地排列球体。尝试思考高维空间可能令人困惑,但数学家们为此掌握了一些技巧。正如三维空间可以使用三个坐标——长度、宽度和高度,或 (x,y,z)——来标记一样,八维空间使用八个坐标。我们可以通过添加更多坐标来研究的维度数量没有限制。在任何维度中,球体都是一组到某个中心点距离都相同的点。在二维空间中,球体是一个圆,在三维空间中,它是我们通常认为的球体。
由于高维空间对于我们来说即使不是不可能可视化,也很困难,因此很容易认为它们没有任何现实世界的意义。然而,令人惊讶的是,它们可以非常自然地出现。
它们自然出现的一种方式是在缝纫中,这是我本月早些时候写过的。在我的关于维亚佐夫斯卡球体堆积突破的文章中,我提到了高维球体堆积的另一个应用:数据传输和纠错码。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们今天世界的发现和想法的具有影响力的故事的未来。
情况如下:我们想通过一个信道传输消息,数据在传输过程中可能会损坏。在现实世界中,想想手机或光纤电缆,甚至只是试图在嘈杂的房间里进行对话。我们的想法是找到一种通信方式,使其能够抵抗传输数据中的微小变化。
以 北约音标字母为例,它更广为人知的名称是它的前三个词,alpha-bravo-charlie。如果您必须通过电话拼写您的名字,那么另一端的人很容易将 B 误认为 P,因此能够说“B 代表 bravo”很有帮助。音标字母中代表字母的单词经过选择,即使有很多静电,也不会对您指的是哪个字母产生任何歧义。您永远不会说“B 代表 bad”,这可能会让对方感到困惑:“D 代表 dad?P 代表 pad?”
纠错码就像音标字母一样,是一种编码数据的方式,即使数据在传输过程中被更改,也允许人们重建消息。 一种方法是仅选择有限数量的可能消息进行传输,并构建一些冗余。 例如,如果我们只想传输消息“yes”和“no”,我们可以决定将“yes”编码为 111,将“no”编码为 000。 如果我们收到消息“101”,我们可以假设其中一个数字在传输过程中已损坏,但仍然可以推断出发送者打算说“yes”。 当然,此代码并非完美。 如果两个数字被损坏,我们将最终误解答案,但这肯定比没有好。
当我们尝试为发送更复杂的消息寻找纠错码时,球体堆积就派上用场了。 在这种情况下,我们可以将我们正在传输的数据视为高维空间中的一个点。 例如,如果我们想传输每条消息包含 100 条数据的消息,我们可以将我们的消息视为 100 维空间中的点。 每个坐标都是其中一条数据。
我们的目标是在 100 维空间中找到一组好的点,我们可以将其用作码字。 我们希望我们的码字做什么? 好吧,如果某些数据片段略有更改,我们希望码字仍然可以识别,因此我们不希望我们的码字太相似。 在 100 维空间中,这相当于每个码字都是一个具有某个小半径的 100 维球体的中心。 发送消息的人将传输其中一个球体中心的坐标作为他们的码字。
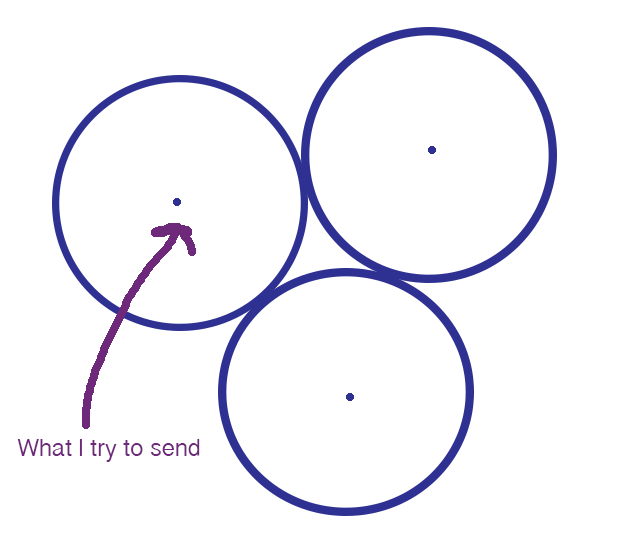
我还没有获得可以绘制 100 维球体的 Adobe 升级版,因此这张二维示意图将不得不凑合使用。 图片来源:伊芙琳·兰姆
如果点的坐标在传输过程中略有更改,则接收者将收到与发送者发送的消息略有不同的消息。
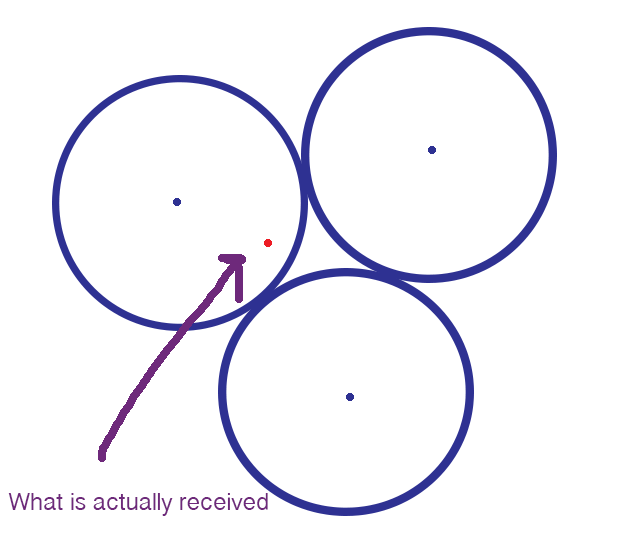
图片来源:伊芙琳·兰姆
但是,如果消息仍然非常接近预期消息,则接收者将知道预期消息是什么并正确解释消息。 幸运的是,在上面的图表中,错误消息与我打算发送的消息之间的距离很小,因此接收者将正确解释它。
球体堆积问题询问我们如何在例如 100 维空间中尽可能密集地堆积等尺寸的球体。 对于纠错码,这些球体的中心是我们的码字。 半径的选择将基于我们认为我们的传输方法可能会在发送消息时晃动消息的程度。 如果我们认为错误的累积效应——每个点在传输中可能被推离多远——最多为 1 个单位,我们将考虑堆积半径为 1 的球体。 如果可能是 3 个单位,我们将堆积半径为 3 的球体。 但是,半径是多少并不重要。 这是一个数字,我们将根据我们的传输技术的工作方式来选择它。
因此,我们正在寻找 100 维空间中的球体,它们的半径彼此之间都相距一定距离。 惊喜! 我们刚刚在其自然栖息地中找到了一个球体堆积问题。 解决 100 维空间中的球体堆积问题相当于弄清楚我们可以在 100 维空间中的某个定义区域中堆积多少码字。 我们堆积码字的效率越高,我们可以使用我们的 100 维消息方案发送的独特消息就越多。 这就是为什么解决球体堆积问题可能对数据传输产生重要的实际影响。
人们可能会合理地问,解决球体堆积问题对于寻找纠错码有多重要。 我们看到球体堆积问题是解决纠错码的一种方法,但也许我们是否找到最有效的方法来堆积它们并不重要。 相当好就足够了吗?
高维球体变得尖锐。 这是一种异想天开的方式来描述关于高维球体的两个相关事实:直径为 1 的球体在我们维度升高时,在边长为 1 的立方体的体积中所占的比例越来越小,并且最佳球体堆积的密度随着维度的增加而降低。 在二维空间中,我们可以用蜂巢式最佳六边形堆积用圆填充大约 91% 的平面。 有效堆叠的橘子可以填充大约 74% 的三维空间。 球体堆积问题在四维空间中尚未解决,但在八维空间中,维亚佐夫斯卡表明,最密集的堆积填充了大约 25% 的空间,而在 24 维空间中,最佳堆积仅填充了 0.1% 的空间。 事实上,虽然我们不知道除二、三、八和 24 维之外的任何维度的确切答案,但我们确实知道球体堆积密度的上限随着维度的增加呈指数级下降。
高维球体的尖锐性意味着,即使在 100 维空间中有很多空间,当我们尝试制作纠错码时,我们也不能很好地将码字塞进去。 因此,找到最佳球体堆积变得更加重要,这样我们才能尽可能多地从(或进入?)难以填充的空间中获得。
维亚佐夫斯卡在八维球体堆积方面的突破——以及随后的 24 维问题解决方案——对使用这些维度创建纠错码没有实际影响。 研究人员已经知道正确答案在百分之几的误差范围内,因此任何在这些维度中堆积球体的人都已经使用了正确的模型。 但她的工作证明了一种新颖的球体堆积方法有可能在其他维度上发挥作用,并对我们彼此沟通的方式产生重大影响。