本文发表于《大众科学》的前博客网络,反映作者的观点,不一定反映《大众科学》的观点。
我一直认为《蒙娜丽莎》作为连点成线谜题会更好,难道你不觉得吗? 幸运的是,对我们来说,欧柏林学院的数学家罗伯特(鲍勃)·博世和计算机科学家汤姆·韦克斯勒正在开创一种新技术,可以将您最喜爱的杰作变成由点和交叉线组成的复杂图案。他们称之为具象巡回问题(FTP)。他们关于该方法的初步论文将发表在2015 Bridges数学-艺术会议的论文集中,目前可在博世的网站上在线获取。
这项新技术是对现有优化艺术流派的扩展。 优化艺术使用计算约束来生成有趣的图像。多米诺骨牌肖像和马赛克是一种形式,但与FTP最接近的优化艺术类似物是旅行商问题(TSP)艺术。旅行商问题的目标是找到穿过任意一组点的最短路径,就像旅行推销员在可以轻松建立Etsy商店之前的黑暗日子里可能走过的路径一样。
为了创作TSP艺术,您需要将所需的图片变成一片聚集的点,然后让计算机找到它们之间TSP最优路径,如下图所示。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您将有助于确保未来能够继续报道有关发现和塑造我们当今世界的想法的具有影响力的故事。

左图:蒙娜丽莎TSP的点簇。右图:最优路径。 来源:罗伯特·博世和汤姆·韦克斯勒
正如博世和韦克斯勒写道:“即使这条路径是可能的最佳路径,并且确实与目标图像相似,但它并没有像单独的点那样达到良好的相似度。” 仅仅为了让图片变得更糟而解决旅行商问题似乎有点浪费,因此他们决定改变游戏规则。
他们没有在图像中聚集点,而是从规则的点网格开始。然后,游戏的目的是将它们连接起来,不是用解决旅行商问题的路径,而是用在视觉上类似于目标图像的路径。路径仍然应该精确地击中每个点一次,但现在获胜的行程可能会比TSP最优路径更长。
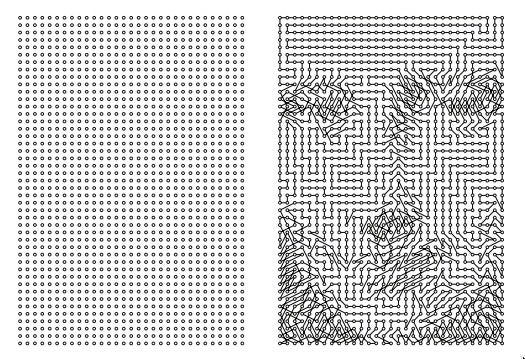
左图:1395个点的网格。右图:类似于蒙娜丽莎的具象巡回。 来源:罗伯特·博世和汤姆·韦克斯勒
为了量化这个问题,博世和韦克斯勒将目标图像转换为灰度图像,并为网格的每个点分配一个介于0和1之间的数字,该数字表示图片在相应区域的深浅程度。经过一些实验,他们决定将边缘限制为国王或骑士的移动,并且进一步的实验帮助他们确定如何为网格的每个部分分配权重,以对应边缘使其变暗的程度。研究人员使用Gurobi优化器来寻找路径,以最大限度地减少灰度目标图像和FTP图像之间亮度的总差异。

波提切利的《维纳斯》作为具象巡回。 来源:罗伯特·博世和汤姆·韦克斯勒
正如您可能想象的那样,具象巡回问题在计算上非常昂贵。 事实上,对于他们使用的网格尺寸,Gurobi 根本无法获得良好的结果。(“我不是在责怪Gurobi,”博世在一封电子邮件中写道。这是一个难题!)博世和韦克斯勒没有尝试在整个网格上优化路径,而是决定分别查看较小的块,然后仔细地将他们为每个部分获得的路径拼接在一起,以找到整个网格的良好解决方案。 这个过程仍然需要很长时间,但至少它可以发生。“使用滑动窗口方法,我可以在一两天内获得一个像样的具象解决方案,”博世写道。
博世和韦克斯勒的论文还描述了一种类似的新优化艺术方法,称为具象编织问题:他们不是用一条路径连接网格中的所有点,而是在顶行的每个点开始一条路径,并最终将每个顶部点连接到底部的一个点,在向下移动的过程中精确地击中每行中的一个点。 这些线束彼此分离,因此,像辫子的线束一样,它们从上到下交织在一起。 在我看来,这些图像看起来并不像FTP解决方案那样像目标图片,但弯曲的线条很独特且在视觉上令人愉悦。 它们非常适合放在宿舍的墙壁上。

玛丽莲·梦露作为具有三种不同约束条件的具象编织问题的解决方案。 来源:罗伯特·博世和汤姆·韦克斯勒
对于理论计算机科学爱好者:博世尚未研究FTP的计算复杂性,但他的猜测是它是NP-hard难题。 这也是我的猜测;它似乎与TSP没有太大区别——只是优化的函数略有不同,但问题的关键是相似的。 这只是一个猜测,但我喜欢绘制蒙娜丽莎是NP-hard难题的想法。
