本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点

一个牙膏管具有二维洞的演示。图片来源:Slipp D. Thomson,通过 Flickr。
万圣节时,我写了一个非常可怕的话题:高阶同伦群。同伦是拓扑学中的一个概念,拓扑学是数学的一个分支,研究形状的属性,这些属性无论你如何挤压或拉伸它们都保持不变,只要你不撕裂它们或将东西粘在一起。同伦群和稍微相关的同调群都是用代数描述形状拓扑的不同方法。在我的文章中,我说同调检测不同维度的“洞”。但是,正如一位评论员所问,我说的不同维度的洞是什么意思?
好问题!我故意使用“洞”作为一个含糊的词,因为“洞”没有真正的数学定义。但这是我的简短回答,这也是我不是代数拓扑学家的原因。如果你可以把它放在项链上,它就有一个一维的洞。如果你可以用牙膏填充它,它就有一个二维的洞。对于更高维度的洞,你就只能靠自己了。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够持续讲述关于发现和塑造我们当今世界的想法的具有影响力的故事。
这个答案不是很令人满意。有没有更好的方法来描述洞?我和我的一些拓扑学家朋友交谈,发现了两件事:拓扑学家们对洞的定义并不完全一致,思考一个数学定义尚未完全确定的词的不同解释是既有趣又令人感兴趣的。我认为我更大的结论,本着这个季节的精神,是洞就像圣诞老人:真正的意义在于你的心中。所以让我们审视我们的内心,思考洞是什么。
《斯坦福哲学百科全书》中有一篇关于罗伯特·卡萨蒂和阿基莱·瓦尔齐撰写的有趣的关于洞的条目。它开头是
对于本体论学家和认识论学家来说,洞是一个有趣的案例研究。对世界的天真、未经教导的描述将洞视为指称的对象,与普通的物质对象相提并论。(“奶酪上的洞和锡罐里的饼干一样多。”)我们经常求助于洞来解释因果互动,或解释某些事件的发生。(“水流出来是因为桶上有个洞。”)因此,有初步的证据表明这些实体的存在。然而,可能会有人认为,提到洞只是一种说法,洞只是纯粹的表象实体,类似实体,虚构。
幸运的是,我们是数学家,而不是哲学家,所以我们不需要过多地担心洞是否存在这种琐碎的细节。(有些人也对圣诞老人采取这种态度。)
我必须警告你,这篇文章最终会有点循环论证。在某种意义上,n维洞的数学定义“应该”是导致n维同调群或同伦群中存在有趣的东西,或使其非平凡的东西。

一个篮球上有一个洞。图片来源:公共领域,通过维基共享资源。
Mathworld关于洞的条目中,埃里克·韦斯坦给出了一个我非常喜欢的定义:“数学对象中的洞是一种拓扑结构,它阻止该对象被连续地缩小到一个点。”
让我们想想一个篮球。使用韦斯坦的定义,它肯定有一个洞,因为你不能在不改变其篮球性的情况下将其完全挤压成一个点。
我喜欢这个定义,因为它很直观,但我认为它有点危险,因为拓扑学中使用了几种不同的连续缩小到点的概念,并且很容易将它们混淆。(相信我。我经历过。)平面中的一个圆可以连续地缩小到一个点*,但直观上,并且在同伦和同调的意义上,一个圆有一个洞。然而,这种缩小的概念依赖于圆位于二维平面中的假设,所以它实际上告诉我们一些关于平面的拓扑结构,而不是圆的拓扑结构。我们需要我们的定义不依赖于事物在空间中的位置。
韦斯坦的定义使用的缩小到点的概念要求我们始终保持拓扑等价。我们不能将一个圆缩小到一个点,因为我们最终会在最后撕裂或挤压某些东西。
那么定义洞的维度呢?这更棘手。一个诱人的定义,也是我一位拓扑学家朋友更喜欢的定义,是流形中的n维洞是流形“像”n维球体的地方。(为了我们的目的,一维球体是一个圆,二维球体是篮球形状,依此类推。这是因为近距离观察,圆看起来像一条线,球体看起来像一个平面。)更严格地说,对象中的n维洞是阻止n维球体到该对象的某些映射在不离开该对象的情况下缩小到一个点的东西。洞的这个定义意味着我们将洞性等同于同伦。让我们研究一些例子。
首先,一个平面。你不能把它放在项链上,也不能用牙膏填充它,所以它可能没有洞。让我们检查一下。有很多不同的方法将一个圆映射到一个平面,但所有这些方法都可以在保持在平面上的同时缩小到点。换句话说,在平面上滑动橡皮筋并尽可能缩小它没有任何阻碍。所以根据我们目前的工作定义,平面没有一维洞。这很好,因为如果平面有一个洞,那么我们对洞的定义就是错误的。
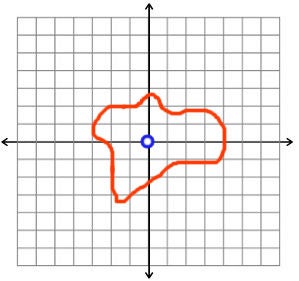
我们可以判断穿孔平面有一个洞,因为我们无法将橙色环拉过缺失的点,蓝色轮廓突出显示了缺失的点。图片来源:伊芙琳·兰姆。
那么移除一个点的平面呢?我们仍然不能用牙膏填充它,但是如果给定一条非常细的链条,我们可以把它放在项链上,所以它应该有一个一维洞。我们如何看到这一点?如果我们将一个圆映射到平面上,并且移除的点在圆内,我们就会遇到问题。(书呆子可能会指出,我没有证明存在圆映射到平面内部和外部这样的东西,无论有没有洞。你是对的,你可以自己写一篇关于它的博客文章。我们其余的人会假设我们可以找到一个足够礼貌的圆映射,使其具有明确定义的内部和外部。)我们无法将圆拉过或缩小到该点,所以我们知道减去一个点的平面有一个一维洞。
现在回到我们之前谈到的篮球。我们知道它有一个洞。它的洞是什么维度?你不能把它放在项链上,但你可以用牙膏填充它,所以它可能是二维的。现在来检查一下。它没有一维洞,因为任何你把橡皮筋(或圆)放在篮球上的方式,你都可以把它缩小到一个点,而不会离开篮球的表面。但它确实有一个二维洞,因为你不能连续地将二维球体到该空间的每个映射都缩小到一个点,而不离开篮球。(为了选择唾手可得的成果,如果你的从篮球到篮球的映射是恒等映射,即所有东西都停留在同一个位置,你就无法将其缩小到一个点。)
到目前为止,我们使用的洞的定义似乎很有希望。但最终,我认为它不是最好的定义。
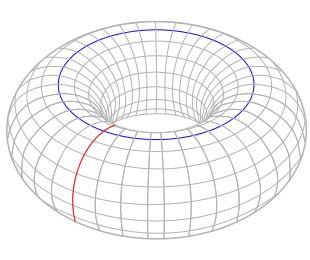
环面上的两个突出显示的环向我们展示了两个不同的一维洞。图片来源:YassineMrabet,通过维基共享资源。
让我们看看环面,最简单的拓扑空间之一。环面可以被认为是甜甜圈的釉或内胎的表面。我们可以把它放在项链上,也可以用牙膏填充它,所以它应该有一维和二维的洞。对于一维洞来说,一切都很好:基本上有两种主要的圆的映射无法缩小到环面上的一个点的方式。要么它可以绕着甜甜圈的洞(左图中的蓝色圆圈)转,要么它可以像你的手指如果穿过甜甜圈的洞并用你的食指抓住它所形成的圆圈(左图中的红色圆圈)。所以环面有两个一维洞。(除非你站在环面内部佩戴其中一条项链,否则你不会用项链定义找到它们。)
当我们涉及到二维洞时,我们的工作定义就崩溃了。环面“应该”有一个二维洞,但我们无法使用二维球体的映射找到它。(这至少对我来说并不明显。你可以考虑尝试用气球包裹内胎,以了解正在发生的事情。)
我们根据球体的映射对洞的定义不适用于环面中的二维洞,但我真的想说洞在那里。我认为正确的答案,尽管它看起来不是特别有见地,是使用相同的定义来定义洞,但允许任何二维物体的映射,而不仅仅是球体。有一个二维物体我们可以映射到环面中,而不能在保持在环面上的同时缩小到一个点,它就是环面本身。所以如果我们知道环面在拓扑上不等同于一个点,我们就知道它有一个二维洞。这种定义看起来有点像“我看到它时我就知道它”的定义,并且在实践中没有太大帮助。如果我们对一个物体知之甚少,我们如何知道要将无限多的二维表面中的哪一个映射到其中以测试其圣洁性?但是这种概念的一个版本,更精确地定义,就是同调。(对于有雄心壮志的人,你可以在艾伦·哈切尔的免费代数拓扑教科书中阅读更多关于它的内容。值得注意的是,哈切尔始终在“洞”这个词周围使用引号,因为他从未定义过它。)
定义同调有几种方法,但对我来说最直观的方法是采用一些基本构建块——顶点、边、面等等——并观察它们如何粘合在一起形成表面。虽然它比这更微妙,但同调基本上告诉你某种维度的哪些构建块没有限定你空间中更高维度的构建块。这与我们已经看到的洞的概念相符:环面中的两个不同的洞来自(一维)圆,这些圆没有围绕空间中的(二维)实心圆盘转动。二维洞来自于环面仅由二维和更小的组件组成的事实,因此其二维组件不限定表面的任何三维部分。另一方面,实心环面(整个甜甜圈)没有任何二维部分不是三维部分的边界,因此它没有二维洞。(甜甜圈釉的二维洞现在被三维面包填充。这比牙膏好多了。)

霍普夫纤维化的可视化,这证明了一个令人惊讶的事实,即篮球有一个三维洞。图片来源:Niles Johnson,通过维基共享资源。
数学家通常仅将同调称为检测洞,使同伦——以及我们早期对n维洞的工作定义——高高挂起。这个定义的一个优点是,我们永远不会在低维空间中有一个高维洞,这是一个令人不安的前景,这也是我发现高阶同伦群令人毛骨悚然的原因。如果我们允许基于同伦的洞的定义,那么篮球就有一个三维洞。(所以我猜它可以被四维生物用来刷牙。)霍普夫纤维化,我在之前的文章中也提到过,是从三维球体到二维球体的映射,它不能缩小到一个点。
所以对于洞,你可以选择你最喜欢的定义。我想我更喜欢使用同调定义,但是关于不同的洞检测器可以检测到不同的洞的想法有一些美妙之处,所以我可能会尝试敞开心扉——为了简单起见,我假设它在拓扑上等同于一个二维球体——并让三维洞进入。
如果你坚持到这里,你值得一份奖励。一个装满西瓜果肉的二维球体没有一维洞的演示怎么样?
感谢Arunima Ray和两位克里斯托弗·戴维斯(Christopher Davis?)对这篇文章的有益评论。任何你不喜欢的地方都是我的错。
*在平面中将圆缩小到一个点的秘诀:从半径为 1 的圆开始,为了方便起见,将其设置在点 (0,0)。我们将定义一个双变量缩小映射。第一个变量将表示圆上的一个点,我们将通过角度(从 x 轴逆时针测量)来识别它。第二个变量表示时间。我可以使用映射F(a,t)=(1-t)a在从 0 到 1 的时间间隔内将任何圆缩小到一个点。在严格介于 0 和 1 之间的任何时间w,此映射的图像都是半径为1-w的圆。在时间 1,我们有一个半径为 0 的“圆”,这也称为一个点。像这样的映射一直被用作路径之间显式同伦的示例。