本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
我对连分数了解得越多,就越为之着迷。 上周,当我写到连分数比我们通常用来描述数字的任意十进制数字好多少时,我提到连分数告诉我们无理数的“最佳逼近”。 连分数只是由分数组成的分数。 每个数字,无论是有理数还是无理数,都可以写成连分数。 为了获得编写它们的系统方法,现在我们将专注于分子中只有 1,分母中只有正整数的连分数,尽管有些非常漂亮的连分数不具有此属性。
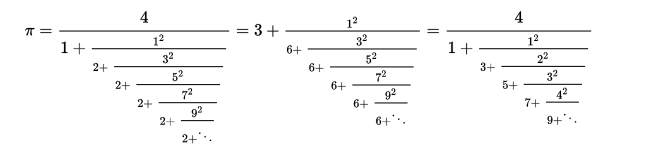
一些不遵循我们规则的漂亮的 pi 连分数表示。
我们将研究看起来像这样的连分数。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您将有助于确保未来继续产出关于塑造我们今天世界的发现和想法的具有影响力的报道。
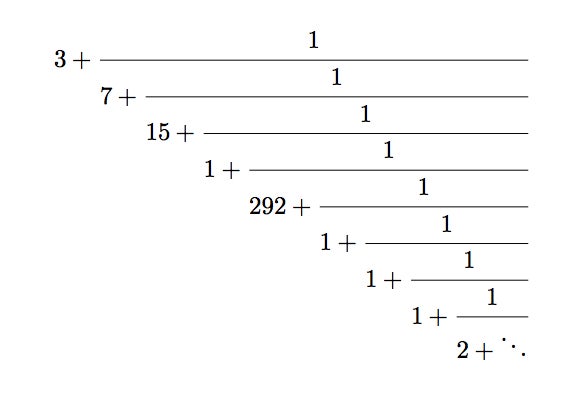
符合我们规则的数字 pi 的连分数表示。
当我们在有限项后截断连分数时,我们得到所谓的收敛。 数字的连分数表示中的收敛是该数字的最佳有理逼近。 但是我们需要考虑这意味着什么。 没有所谓的最接近无理数的有理逼近。 通过增加分数的分母,我们可以根据需要尽可能接近。 截断数字的十进制表示是做到这一点的一种方法。 如果我们想获得更好的数字逼近,我们可以添加更多十进制项。 因此,任何关于“最佳逼近”的合理想法都是相对的。 它需要考虑分母的大小。
在 A. Khinchin 的关于连分数的经典著作中,他定义了数字“最佳逼近”的两个概念。 第一个更容易描述:如果分数 c/d 比任何分母较小的数字更接近 a,则分数 c/d 是数字 a 的最佳逼近。 也就是说,对于任何其他分数 p/q,如果 q
所有连分数收敛都是第一类最佳逼近,但它们满足比这更强的属性。 基本思想是,如果你让分母更大,你会在某种程度上付出代价。 这可能是将披萨切成如此小的块(或者你那样切时损失的奶酪)的难度,可能是进行计算所需的计算能力,可能只是写出数字需要多少墨水和精力。 但是是有代价的。 如果我们要在分母上付出这个代价,我们希望我们的最佳逼近真的很好。 我们不只是想要比我们得到的最后一个好的逼近稍微好一点的东西,我们想要一些值得为分母付出代价的东西。
数学条件是这样的:对于数字 a,如果对于每个其他分母 q
让我们看看它在 pi 中是如何工作的。 USC 信息科学研究所的 John Heidemann 有一个包含所有分母高达约 5 千万的 pi 的最佳有理逼近(第一类)的列表。 数字 3/1、13/4、16/5、19/6 和 22/7 是此列表中的前几个分数。 13/4 比 3 更接近 pi。 它大约相差 0.1084 而不是 0.1416。 但是,如果我们将差值乘以分母,则 13/4 效果不佳。 我们得到 0.1416×1=0.1416 和 0.1084×4=0.4336,因此 13/4 输得很惨。 16/5 和 19/6 也是如此。 它们都更接近 pi 一点,但它们不够接近以弥补它们较大的分母。 因此,13/4、16/5 和 19/6 是第一类最佳逼近,但不是第二类最佳逼近。 但是,当我们到达 22/7 时,情况发生了变化。 它非常接近 pi。 它的差值 0.00126 非常小。 如果我们将其乘以其分母,则得到 0.00126×7=0.00882。 这很容易击败 0.1416,因此它是第二类最佳逼近。 它也是 pi 的连分数中的下一个收敛。
我最喜欢的 pi 的连分数收敛是 355/113。 这是一个非常好的逼近。 这是一个连分数的完美示例。 第一类下一个最佳逼近的分母为 16,604。 但它甚至没有比 355/113 好多少。 我们没有获得另一个十进制数字的精度,但我们必须将分母增加两位十进制。 不用了,谢谢。 我们必须增加到分母 33,102* 才能获得一个新的值得关注的逼近。
下一个逼近 103,993/33,102* 对应于当我们在 292 处截断 pi 的连分数表示时得到的收敛。 这导致了一个有趣的定性观察:数字的连分数中的大分母告诉你,你之前得到的收敛确实是一个非常好的逼近。 (记录在案,“非常好的逼近”不是一个技术术语。)另一方面,小分母意味着先前的收敛不是那么好。 当你考虑分数是如何工作时,这是有道理的。 大分母意味着我们只需要添加一小片东西就可以更接近我们的目标。
所有连分数收敛都是第二类最佳逼近,因此我们可以将它们视为最佳逼近中的最佳。 这些逼近的分母与仅仅是最佳的逼近(即第一类最佳逼近)之间存在一些有趣的关系。 这有点复杂,但一个有趣的结果是,为了获得不是第二类最佳逼近的第一类最佳逼近,连分数必须具有除 1 以外的分母。 因此,黄金比例(其连分数仅由 1 组成)只有第二类最佳逼近。 它的所有逼近都是最佳中的最佳。 另一方面,由于所有这些 1,它的最佳逼近是最差的,即使是最佳逼近也可能是最差的。 你甚至可以说黄金比例具有最佳中的最佳中的最差逼近。 或者可能是最佳中的最佳中的最差逼近。
连分数是关于卓越的。 我们不会满足于平庸的数字逼近(十进制——呸)甚至仅仅是最佳的逼近。 只有最佳中的最佳才能满足,只有真正值得写下来的数字。

保持渴望。
*这些数字在发布后已更正——我不小心高估了 pi 收敛!