本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定代表《大众科学》的观点
上周日,我写了我在ScienceOnline上的公共统计会议。今天,我将向您介绍我的另一个会议,动手数学,由Matthew Francis共同主持。如果您参加我们的会议,您可能会带回家一个属于您自己的数学曲面。
认识一下艾莉。她看起来可能像一个形状奇怪的枕头,但她远不止于此。

艾莉,一个亏格为 2 的曲面。更多的枕头应该有亏格。 图片来源:Evelyn Lamb
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保未来继续产出关于塑造我们当今世界的发现和思想的、有影响力的报道。
首先,艾莉是一个亏格为 2 的曲面。她有两个孔,您可以在这张照片中看得更清楚一些。

艾莉的俯视图,展示了她确实具有亏格 2 的事实。图片来源:Evelyn Lamb
曲面在数学中随处可见,而艾莉是一个非常有趣的曲面,有很多属性值得探索。例如,她是一个平移曲面。这些曲面是通过在欧几里得平面上取一个多边形(在本例中是一块 L 形的织物),并将相同长度的平行边粘合(或缝合)在一起而形成的。

一块 L 形织物,标有标识,使其成为平移曲面。具有相同符号的边将被缝合在一起。图片来源:Evelyn Lamb
我将让 Diana Davis 的 "用舞蹈演绎你的博士论文" 视频用另一种方式解释它。
双五边形上的切割序列,通过舞蹈解释,来自 Diana Davis,发布在 Vimeo 上。
在第一个场景中,每当舞者穿过双五边形的边缘之一时,她就会在屏幕的另一部分重新出现,因为我们要想象这个图形是被粘合起来的,相同颜色的边被识别出来。
平移曲面本身就很有趣,但当我们研究多边形上的台球时,它们也会自然而然地出现。例如,在 L 形的台球桌上,母球可以采取什么样的轨迹?信不信由你,我们可以研究像艾莉这样的曲面来找出答案。顺便说一句,这并非完全是学术性的练习:数学家 Moon Duchin 实际上在南非旅行时偶然发现了一张这样的 L 形桌子。
一个普通的单孔环面是平移曲面的另一个例子。在这种情况下,多边形是正方形或矩形。
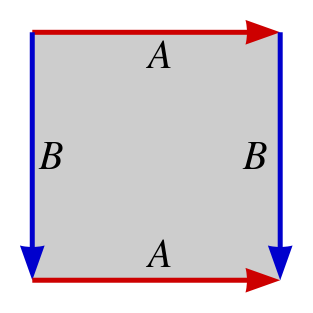
一个正方形,顶部和底部边标记为“A”,左右边标记为“B”。通过将具有相同标签的边以及对齐的箭头粘合在一起,制作一个环面。图片来源:Ilmari Karonen Wikimedia (公共领域)
此动画显示了粘合过程

一个正方形卷成一个圆柱体,然后卷成一个环面。图片来源:LucasVB Wikimedia (公共领域)
我们可以看到,无论我们站在环面的哪个位置,我们周围的地面都非常平滑。那是因为如果我们看看正方形的角会发生什么,它们都被识别在一起,但它们周围正好有 360° 的角度。对于 L 形桌子,情况有点不同。再一次,所有的角都被识别为同一点,但现在我们在这个点周围的角度远远超过 360°。

当进行识别时,所有蓝色顶点最终都被识别为同一点。蓝色点周围的绿色弧线帮助我们计算该点周围的角度量。在这里我们可以看到,我们有三个圆的角度,1080°。图片来源:Evelyn Lamb
那个有趣的、难以拍摄的点通常被称为锥点。我制作艾莉是因为我想拥有一个可触摸的曲面模型,它有点像我研究的那些具有这些有趣的锥点的曲面。她与我的曲面并不完全相同,因为她的皮肤是以无聊的欧几里得平面而不是我使用的更性感的双曲平面为模型。但我没有任何用双曲钩针制成的巨大织物片,而且双曲曲面无论如何也无法完全放入三维空间,所以艾莉是我拥有的最接近的东西。
这使我们回到这篇文章的目的:邀请您来到有趣的数学世界,您可以在我们的动手数学会议上制作和触摸数学。我们将讨论我在这里提到的一些主题:拓扑学、几何学和动力系统,我们将用织物和纸张制作曲面。Matthew 是一位物理学家,他将介绍这些数学概念在物理学中出现的一些方式。
如果您认为您可能会参加会议,如果您能在wiki上告知我们,我们将不胜感激。我知道这些决定通常是在最后一刻做出的,这完全没问题。但是,大致了解感兴趣的人数将有助于我们带上适量的织物。如果您不能来,您可以在 Twitter 上使用标签 #HandsOnMath 关注我们。