本文发表于《大众科学》的前博客网络,反映作者的观点,不一定代表《大众科学》的观点
去年,莫斯科国立大学的数学家奥尔加·弗罗尔金娜证明了,在三维空间中,你只能放置可数个不相交的莫比乌斯带。我为《量子杂志》撰写了关于她的工作和一些推广的文章。
如果你还没有接触过可数和不可数无限的概念,它们基本上就是它们听起来的样子。数学家已经证明并非所有的无限都相等。一种无限是当你开始计数并且永不停止时得到的无限:1、2、3、4、…。这被称为可数。任何你可以放入一个列表,并具有第一个元素、第二个元素等等的东西都是可数的。另一方面,没有办法列出实数,甚至只是 0 和 1 之间的实数。你制作的每个列表都会是不完整的。(要了解原因,请阅读Yen Duong 的这篇文章。)因此,实数是不可数的。当你体验过实数的丰富性时,说实话,可数无限听起来有点微不足道。只有微不足道的无限个莫比乌斯带可以放入三维空间。
当我在撰写《量子杂志》的文章时,佐治亚理工学院的数学家丹·马加利特告诉了我一个关于平面上字母的类似问题。在平面上放置可数个任意字母并不难,因为你可以将它们放在无限网格上,这是可数的。但是对于某些字母,如果你足够聪明,你可以在平面上放置不可数多个副本。
关于支持科学新闻
如果你喜欢这篇文章,请考虑通过 订阅来支持我们屡获殊荣的新闻报道。通过购买订阅,你正在帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
最简单的例子是 O。在平面上放置不可数个 O 的方法有很多种,但一种方法是选择一个半径为 1 的圆,并考虑适合其中的所有同心圆。没有两个具有相同中心和不同半径的圆会彼此相交,并且存在不可数多个小于 1 的可能半径,因此我们已经达到了不可数性,我们完成了。
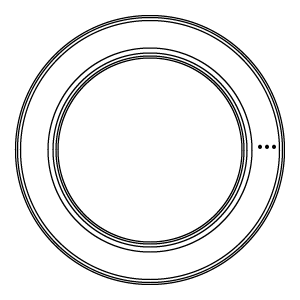
有限数量的嵌套 O。不可数的数量看起来就像一个实心的环。来源:伊芙琳·兰姆
另一方面,平面上只能放置可数多个 X。因此,无限井字棋游戏被限制为可数性,因为 X 阻止了 O 的放置。我们如何知道平面上只能放置可数多个 X?首先,我们可以快速验证我们不能只是将一个 X 放在我们不可数的 O 的每一个里面,因为 X 会最终彼此相交。但是,正如我在关于莫比乌斯带的文章中所写的那样,这个事实并不意味着没有更聪明的方法来放置它们。
为了证明不可能在平面上嵌入不可数多个 X,我们利用了有理数的力量。
我学到的关于可数性最重要的课程,至少在能够证明某些集合是否可数方面,是有理数是可数的。与整数和一些其他可数集合不同,乍一看,有理数是可数的并不明显。它们太多了!在实数线上的任何微小区间内都有无限多的有理数,至少当我第一次看到这个问题时,我认为有理数一定比整数“更多”。我花了很多时间试图证明有理数是不可数的,直到另一位学生给出了它们实际上是可数的证明。将我关于可数集合的默认思维方式从整数(它们间隔很好且显然它们之间有很多空间)转变为有理数(它们到处混杂,但仍然不知何故比实数少),是我数学发展中的重要一步。证明一个集合是可数的一个好策略是找到一种方法来建立该集合和有理数之间的对应关系,而这正是我们可以用 X 来做的事情。
假设我们在平面上有一堆 X。
平面上有限数量的 X。尝试制作无限数量的 X 花费了太长时间。来源:伊芙琳·兰姆
对于每个 X,我们可以找到一个小的圆,其半径为有理数,中心具有有理坐标,使得 X 在四个点处从圆中伸出。在 X 在圆中创建的每个象限内,我们可以找到一个具有有理坐标的点。
.png?w=196)
带有紫色模板的 X。来源:伊芙琳·兰姆
所以每个 X 都有 11 个有理数与之关联:一个用于半径,每个具有有理坐标的点都有两个。正如比尔·拉塞尔所知,11 有点笨重。幸运的是,作为数学家,我们不需要做任何像将它们戴在手指上之类的实际事情。我们只需要知道它们存在,并且如果我们真的必须这样做,我们可以列出它们。
当我和他交谈时,马加利特称圆和有理点为 X 的“模板”。(请注意,每个 X 都有无限数量的潜在模板,因为如果你稍微晃动一个模板,你可以找到另一个有效的模板。)由于这些模板由 11 个有理数定义,因此平面上只有可数多个模板。(我们在这篇文章中没有实际证明这一点,但如果你愿意,你可以自己证明。)因此,如果平面上有不可数多个 X,那么其中无限多个必须具有相同的模板,因为没有足够的不同模板可供使用。最后一块拼图是证明任何两个具有相同模板的不同 X 必然会彼此相交。严格证明这一点并非易事,但如果你开始绘制带有 X 的圆,我认为你可以说服自己。
为了总结一下,唯一的事实是,只有可数多个允许的 X 模板可以在平面上而不相交,这意味着我们只能有可数多个 X。
当我听到这个证明时,我觉得它很可爱,但它也帮助我发展了一些关于莫比乌斯带的直觉。弗罗尔金娜的证明不是基于相同的论证,但它让我更舒服地思考如何甚至处理这样的问题。
其他字母呢?我们可以在平面上放置不可数多个它们吗?对于 C 和 D(无衬线,就像我在本文草稿中使用的字体,而不是本文版本中的字体)的答案是肯定的。对于 X 和 Y 的答案是否定的。对于 V 的答案是肯定的。对于 Q 的答案是否定的;它的右下角有一个类似 x 的部分。我开始发展一些理论,即哪些形状可以在平面上放置不可数多个同类,然后我偶然发现了波士顿大学数学研究生 Sachi Hashimoto 关于此的文章“涂鸦集合论”。当她作为本科生拖延作业时,她开始思考这个问题,并开始思考她看到的一个问题:你可以在平面上嵌入不可数多个 8 字形吗?“如果你真的在拖延你的作业,你就会从那里继续,”她开玩笑说。
她开始涂鸦字母和其他形状,试图找出简单的标准来确定哪些形状可以在平面上嵌入不可数多次,哪些不能。她和她博客上的一位评论者也提出了一些猜想,但从未找到确凿的证据。当我和她谈论这个问题时,她告诉我她希望我能一劳永逸地告诉她答案。没那么幸运。“时不时地,我会坐下来尝试证明它,”她说,但作为一名计算数论学家,这并不是她擅长的领域。如果你想阅读她的猜想并开始自己涂鸦集合论,请查看她的文章。更新,2019 年 3 月 8 日:Hashimoto 和朋友们继续研究哪些形状可以在平面上嵌入不可数多次。查看她关于此的新文章!
当我在撰写《量子杂志》的文章和这篇文章时,我与几位数学家讨论了嵌入不可数多个字母或莫比乌斯带的问题,很高兴看到这个问题在一些非常不同的研究领域的数学家中引起了共鸣。我不确定它对数学家如此广泛吸引力的确切原因是什么,但我可以将其推荐为你在与数学家交谈时可以使用的开场白。
我认为它吸引人的一点是,它利用了可以被认为是“小”和“大”的概念的数学性质。在不给出严格定义的情况下,在某种意义上,X 必须比 O“更大”,因为只有可数多个 X 可以放入平面。同样,在三维空间中,莫比乌斯带比圆柱体“更大”。但“大”和“小”的另一个概念是收缩性,即一个空间是否可以在不丢失某些拓扑信息的情况下缩小到一个点。O 不是可收缩的。这个孔是必不可少的。但是对于 X,你可以将腿推入并得到一个点。再次,在不给出具体定义的情况下,可收缩空间感觉比不可收缩空间“更小”。这个孔可能赋予了一些分量。因此,在字母嵌入的情况下,这些不同的小和大概念以有趣的方式碰撞。
另一种思考这个问题的方式是,它告诉我们的不仅仅是关于物体本身,还包括我们嵌入物体的空间。三维空间对于不可数无限多个莫比乌斯带来说“太小”了,而平面对于不可数无限多个X来说也太小了。这个问题有如此多的微妙之处和角度,而且看起来似乎只需要几分钟的思考就能解决,也许数学家们不断被它吸引也就不足为奇了。如果你有什么事情需要拖延(谁没有呢?),我希望你能享受一下这封涂鸦信带来的乐趣。
