本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
在最近一期我们的播客《我最喜欢的定理》中,我的联合主持人凯文·克努森和我与卡琳娜·库尔托进行了交谈,她是宾夕法尼亚州立大学的一位数学家,专门研究应用于生物学和神经科学的数学。您可以在这里或kpknudson.com收听这一集,那里也有文字记录。
库尔托向我们介绍了佩龙-弗罗贝尼乌斯定理,它来自线性代数领域。正如库尔托在节目中热情洋溢地说道,线性代数是数学的支柱之一。它为建模和理解在许多不同背景下出现的方程组提供了一套强大的技术。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
线性代数研究的中心对象之一是矩阵。 矩阵是一个数字数组,但它远不止于此。这些数字排列成行和列,通常被认为是空间变换的简写表示。例如,变换平面的方法之一是取平面中的每个点,写成 (x,y),并将第一个坐标 x 发送到和 2x+y,第二个坐标 y 发送到 x+y。矩阵
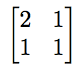
编码了该变换。
一般来说,从原点发出的射线点可以被矩阵编码的变换拉伸和旋转,但在称为特征向量的特殊方向上,变换仅限于拉伸或收缩。没有旋转。指向该方向的单位长度线段被拉伸或收缩的量就是特征值。佩龙-弗罗贝尼乌斯定理指出,对于所有条目均为正数的方阵,存在唯一的最大实特征值,并且其对应的特征向量具有正 x 和 y 坐标。
在与库尔托交谈之前,我隐约记得听说过佩龙-弗罗贝尼乌斯定理,但最初我并没有觉得它特别引人注目。我在我的第一堂线性代数课上很早就了解到,不要对你在矩阵中看到的数字过于在意。也就是说,你不应该认为仅仅根据矩阵条目的外观就可以理解矩阵的作用。我认为我早期未能欣赏佩龙-弗罗贝尼乌斯定理的部分原因是,我对一个允许我根据矩阵中的数字了解变换的定理有点怀疑。更糟糕的是,没有多少矩阵的所有条目都是正数,那么适用于如此排他性矩阵集的定理有什么意义呢?
库尔托让我相信,这个定理比我最初认为的更有用。诚然,没有理由认为任何任意矩阵都将具有全正条目,但许多应用确实主要处理全正矩阵。表示与人口动态、人口统计学、经济学和网络搜索算法相关的函数的矩阵通常具有全正条目,因此佩龙-弗罗贝尼乌斯定理适用于它们。就目前而言,甚至有一个流行病学模型,Kermack-McKendrick 模型,它使用佩龙-弗罗贝尼乌斯定理。(我提到这个模型不应被解释为鼓励大家从事业余流行病学。)想要更广泛地了解佩龙-弗罗贝尼乌斯定理的许多证明和应用的读者和听众应该查看一篇名为《佩龙-弗罗贝尼乌斯定理的许多证明和应用》的论文,这篇论文名副其实,《佩龙-弗罗贝尼乌斯定理的许多证明和应用》。
