本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
学习数学最令人沮丧的事情之一是我们编写教科书和学术期刊文章时,那种掩盖直觉的方式。我们呈现证明的方式并不是我们得出证明的方式——几乎感觉就像作者在掩盖他们的踪迹。
ε-δ 证明是微积分和分析课程中本科生中出了名的不受欢迎的主题。Delta 和 epsilon,两个小的正数,构成了严谨的微积分证明所依赖的支架,而 δ-ε 证明可能是许多数学学生第一次体验到我们呈现数学论证方式的人为性的地方。
δ-ε 证明与微积分中的一个基本概念有关:极限的概念。粗略地说,如果函数的输出可以任意接近 L,只要输入足够接近 p,我们就说函数在点 p 处趋近于极限 L。正如数百万微积分学生多年来一直困惑的那样,我们严格地表述如下:函数 f(x) 当 x 趋近于 p 时,极限为 L,当且仅当对于每个 ε>0,存在一个 δ>0,使得当 x 与 p 的距离在 δ 之内时,f(x) 与 L 的距离在 ε 之内。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
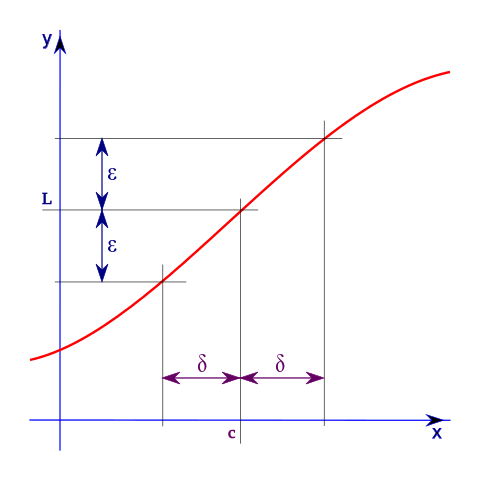
极限的 ε-δ 定义的可视化表示。当 x 与 c 的距离在 δ 之内时,f(x)=y 与 L 的距离在 ε 之内。图片:公共领域 (由用户 HiTe 通过 Wikimedia Commons 提供)。
当您编写 ε-δ 证明时,尤其是作为本科生,您必须满足字面意义上的法律要求。您必须证明,无论给定什么 epsilon,您都可以找出必要的 delta。一个严谨的书面证明以“设 epsilon 大于 0”这句话开头。但是要发现证明,您实际上并不是从 epsilon 开始,而是从 delta 开始。您向输入 x 添加一个任意的 delta,看看函数的输出会发生什么。然后您找出如何使该输出小于 epsilon。
例如,对于简单的函数 f(x)=2x+1,证明的内部心智发现和必要的 delta 将会像这样
|f(x+δ)-f(x)|=|2(x+δ)+1-(2(x)+1)|=|2(δ)|。因此,如果我们想让 f(x+δ) 与 f(x) 的距离在 ε 之内,我们看到 2(δ) 需要小于或等于 ε。因此我们得出结论,δ=ε/2 就足够了。
当我们编写证明时,我们掩盖了我们的思考过程
设 ε>0。设 δ<ε/2。那么 |f(x+δ)-f(x)|=|2(x+δ)+1-(2(x)+1)|=|2(δ)|<2(ε/2)=ε。证毕。麦克风掉落。
对于这个函数的情况,不难看出 2 是从哪里来的,而且证明足够短,任何悬念很快就结束了。但是,即使在这种简单的情况下,delta 优先思考和 epsilon 优先写作之间的视角转换也很困难。
我模糊地记得第一次在高中微积分课上写 ε-δ 证明。今天,我可以看看系数和指数,并很快弄清楚 delta 必须用 epsilon 来表示,但在第一个学期,这感觉就像魔术。在我的证明发现过程的开始,我从不知道最终如何使事情奏效。虽然这个过程有点神秘,但我发现弄清楚 delta 必须是什么,然后写出证明,掩盖我的踪迹,以便我可以在最后得意洋洋地从帽子里拿出 epsilon,这令人满意。
如果 Pi Mu Epsilon 尚不存在,Epsilon Delta 将是数学荣誉学会的完美名称。ε-δ 证明是进入数学证明写作者秘密社团的入门仪式。