本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
今天晚上最令人兴奋的事情是一艘船。在我们住在这里的两个月里,我们公寓隔壁的博物馆在门前摆放了一艘巨大的船,作为他们“Aventuriers des mers”展览的一部分。展览于周日闭幕,今天他们收拾了船。
虽然我会想念这艘船以及它让指路变得多么容易(“沿着塞纳河走,直到你看到那艘巨大的船。不,不是在水上。在人行道上。”),但移走这艘船是期待和快乐的源泉。那里有一台大型起重机!他们用它吊起了船!这是一个数学和工程学的奇迹。确保起重机和人行道能够支撑重量的计算,工人们执行工作的精确度,当然还有现实生活不通勤的重要事实。这场奇观的协调员需要以正确的顺序理解和计划一切。(点击此处阅读一篇法语文章,了解其前往巴黎的部分旅程,包括部分旅程的视频。)
在所有兴奋之后,工作人员用起重机吊起了一艘船,并将其放在平板卡车上。载着船的卡车必须想办法将船从它停放的公共广场/人行道运到巴黎的道路上。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。

船停放在卡车上。图片来源:伊芙琳·兰姆
我看着船和卡车,以及它们停放的人行道和它们即将行驶的街道之间的障碍物。他们会怎么做呢?卡车及其装载物如何在不撞到树木、建筑设备、城市自行车架或户外雕塑的情况下到达道路?我通过思考卡克亚针问题来缓解我的焦虑。
我不知道以这个问题命名的数学家卡克亚崇一是否是一个特别宁静的人,但卡克亚针问题给了我宁静。这个问题询问的是在二维平面内旋转线段(或针)所需的最小面积。(假设针的宽度为零。)
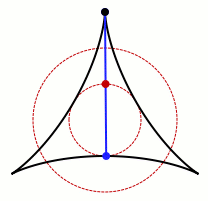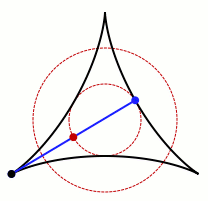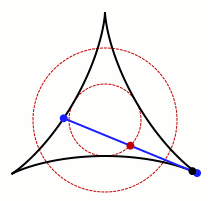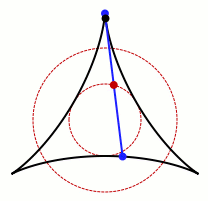
允许卡克亚针旋转的集合的动画。图片来源:Claudio Rocchini Wikimedia (CC BY-SA 3.0)
不难看出,这个过程在圆形、正方形和等边三角形中是可行的。上面的gif也表明,它也适用于非凸形状,即向内弯曲的形状。
卡克亚在1917年提出了这个问题,阿布拉姆·萨莫伊洛维奇·贝西科维奇在1928年解决了这个问题,表明不存在大于0的最小面积。如果你转动得足够慢,在足够长的长度上转动,你将能够使面积小于你想要的任何正数。你可以用铅笔徒手玩卡克亚问题。
我求助于卡克亚问题来寻求安慰,不仅当我在观看平板卡车运载巨型船进行n点转弯时,而且当我在驾驶我的汽车并且需要在狭窄的空间内掉头时。我将卡克亚问题视为驾驶的“如果你能进去,你就能出来”定理,尽管我意识到它们并不完全相同。卡克亚的问题不在乎你是如何到达那里的,它还假设你的汽车是无限薄的,并且你有无限的长度可以利用。驾驶时情况并非如此;尽管如此,我还是允许它让我安心。至少,它提醒我要利用我拥有的空间,并且在转弯时再增加一个点并不丢人。
理论与实践之间的差距有时感觉很大,卡克亚问题也不例外。但是,正如一个在数学考试中被要求“证明或找到反例”的学生可能会告诉你的那样,知道一个问题是可解的,可能是取得进展和决定将你的汽车遗弃在狭窄的停车场或死胡同的尽头之间的区别。因为我知道卡克亚针问题说是有足够的空间,所以我将继续慢慢移动自己,最终会走出去。我不知道移动船的平板卡车司机是否求助于卡克亚针问题来获得勇气,但船最终安然无恙地驶出了,并驶入了巴黎的夜空。
