本文发表于《大众科学》的前博客网络,反映作者的观点,不一定代表《大众科学》的观点
彼得·舒尔茨是 8 月初在国际数学家大会上获得表彰的四位菲尔兹奖得主之一,他研究代数几何。该领域的一个核心问题是多项式方程何时存在整数或有理解。例如,方程 x^2+y^2+z^2=1,它在三维空间中定义了一个球体,有解 (3/13, 4/13, 12/13)。
在他的菲尔兹奖讲座中,舒尔茨谈到了他在 p 进几何方面的工作。(您可以阅读他为配合讲座而撰写的综述文章这里,但坦率地说,如果您能读懂那篇文章,您就不需要阅读我的帖子了,因为您对 p 进数的理解已经远超我了。)p 进数是一种替代的数系,有时比实数更适合解决代数几何和数论中的问题。
有几条道路可以通往 p 进数。其中一种方法是从绝对值开始。我们习惯于标准绝对值,它衡量一个数到 0 的距离。如果一个数大于 0,其绝对值就是它本身,如果一个数小于 0,其绝对值就是它本身的相反数。因此 |1|=1 且 |-1|=1。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保未来有关当今塑造我们世界的发现和想法的具有影响力的故事。
我们可以引入一种不同的方法来衡量数的大小,即基于它与数 p 的关系。如果您上过一些高等数学课,p 可能让您感觉有点奇怪。数学家通常在谈论素数时使用字母 p,并且在本文的其余部分中,我们将假设 p 是素数。当谈论特定 p 的 p 进数时,数学家会用数字本身代替 p,因此我们谈论 2 进数、3 进数、29 进数、314159 进数,您明白了。(是的,314159 是素数。即使我对 π 日嗤之以鼻的心也会为此微微颤动。)
一个数的 p 进绝对值是能整除它的最大 p 的幂的倒数。在这种情况下,一个具体的例子可以使这个复杂的概念更容易理解。让我们先看看 3 进数。数字 4 不能被 3 的任何正幂整除。它等于 30x4。这意味着 1 是能整除 4 的最大 p 的幂,使 4 的 p 进绝对值等于 1/1,或 1。数字 6 有点更有趣。它等于 31x2,使其绝对值等于 1/3。54 的 3 进绝对值是 1/27,因为 27 是能整除 54 的最大 3 的幂。非常大的 3 的幂的倍数具有非常小的 p 进绝对值。
3Blue1Brown 还在这个视频中,用 2 进数的例子解释了 p 进数的概念。
p 进绝对值有一些有趣的性质,而通常的绝对值没有。例如,有很多数字具有相同的绝对值。数字 1、2、4、5、7、8 和其他无限的数字串都具有 3 进绝对值 1。数字 3、6、12、15、21、24 等都具有绝对值 1/3。我们通常的绝对值最多只允许有两个数字具有相同的绝对值。此外,数字不是能够具有连续范围的绝对值,而是具有一组离散的选择。它们有无限多个,但任何数字的大小必须是 p 的幂。因此,没有数字的 3 进绝对值为 1/2 或 7。我们正在以一种奇怪而不同的方式思考数字。
p 进绝对值给我们提供了一种新的方式来衡量两个数字之间的距离。两个数字 x 和 y 之间的 p 进距离是数字 x-y 的 p 进绝对值。因此,回到 3 进数,这意味着如果两个数字的差是 3 的大幂,则它们彼此更接近。数字 1 和 4 的差是 3,因此它们之间的 3 进距离是 1/3。但是数字 1 和 19 的 3 进距离是 1/9 (18=32x2),而 1 和 82 的 3 进距离是 1/81。数字 11 和 29 的差是 18,因此它们的 3 进距离是 1/9。
如果您使用过模算术,这可能会让您感到有点熟悉。在模运算中,或者说模 n,您只关心一个数字与 n 的倍数有多接近。数字 2、9 和 93 模 7 等价,因为它们都比 7 的倍数多 2。在某种程度上,p 进距离给人的感觉是您同时关心所有幂 pk 的模 pk 的数字。
尝试理解新的距离度量方法的一种方法是尝试弄清楚在这种距离中什么与什么接近。在 3 进度量中,正整数彼此之间的最大距离为 1 个单位,因此我们可以将它们都视为生活在这个有界的圆圈中。
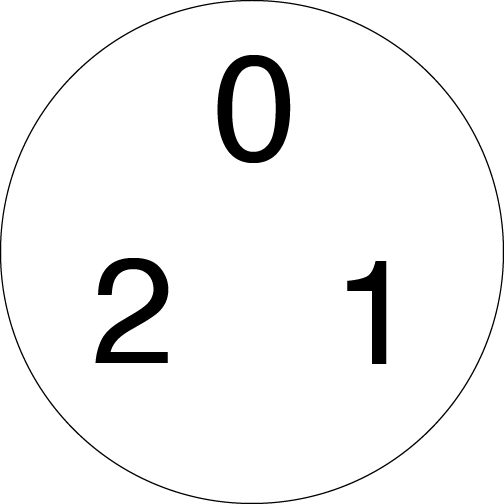
数字 0、1 和 2 位于 3 进数气泡中。所有其他正整数也位于此圆圈中,但如果我们仅从这些数字开始,我们可以以一种简洁的方式看到结构的出现。 来源:伊芙琳·兰姆
让我们将这个圆圈视为意味着圆圈内的任何东西与任何其他东西的距离最多为 1。现在我那里只有数字 1、2 和 3,但是所有大于等于 0 的整数都在那里,因为它们彼此之间的距离最多为 1。
现在我们可以添加另一层。数字 3 距离数字 0 只有 1/3,数字 4 距离 1 只有 1/3,而 5 距离 2 只有 1/3。我们可以将这些数字添加到较小的圆圈中。如果两个数字在同一个较小的圆圈中,则它们彼此之间的距离最多为 1/3。
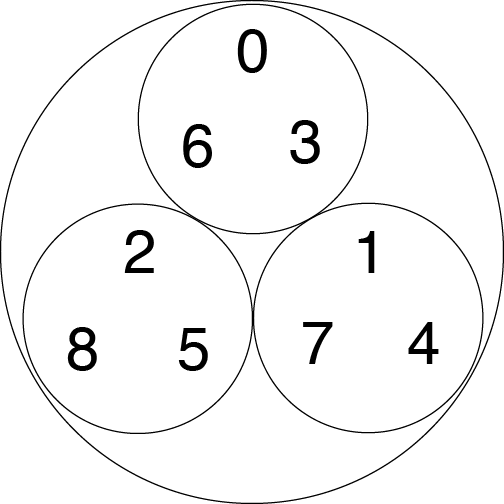
以 3 进数排列的数字 0 到 8。例如,数字 0、3 和 6 彼此之间的距离都为 1/3,因此它们在同一个小圆圈中。来源:伊芙琳·兰姆
我将绘制此过程的另一层,但我们可以永远继续下去,产生一个类似于谢尔宾斯基三角形的美丽分形图案。两个数字之间的距离是包含它们的最小圆圈的大小。
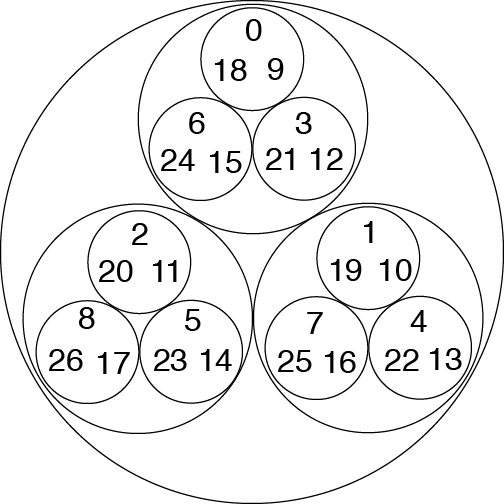
基于数字 0-26 彼此之间的 3 进距离的表示。来源:伊芙琳·兰姆
哇!这有很多工作要做,而且我们甚至还没有超出正整数的范围。但是 p 进数不会止步于此!您可以将 p 进绝对值和距离函数扩展到所有有理数。
一个数的 p 进绝对值基本上衡量它的 p-ishness。p-ishness 越高,数字的绝对值就越小。因此,为了将其扩展到分数,如果分数的分子可以被 p 的幂整除,我们希望 p 进绝对值很小。为了平衡,如果分数的分母可以被 p 的幂整除,则该数具有较大的 p 进绝对值。(我们假设分数以最简形式书写,因为您为什么要以其他方式书写?)数字 1/2 实际上与 3 无关,因此其 3 进绝对值为 1。数字 3/4 的分子中有 3,因此其 p 进绝对值是 1/3,就像 3 本身的 p 进绝对值一样。数字 1/3、2/3 和 5/6 的 3 进绝对值都是 3。数字 1/9、7/9 和 2/63 的 3 进绝对值都是 9,您可以看到规律。非常大的 3 的幂具有非常小的 3 进绝对值,而非常大的 1/3 的幂具有非常大的 3 进绝对值。我们可以想象向上面的 p 进数图添加数字。我不会这样做,但我们可以开始弄清楚在哪里将一些分数添加到上面的 p 进数图中。数字 1/2 在 3 进数中与数字 5 非常“接近”,因为 5-1/2,4 1/2,可以写成 9/2,并且分母中有一个 3 的幂。
这篇文章已经很长了,我们甚至还没有涉及到如何以 p 进数书写数字!如果您好奇,您必须在其他地方查看。您可以从 Cut-the-Knot 的这两个页面开始。这些p 进展开非常酷,在概念上与以 p 为底而不是以 10 为底书写数字相关,但又有所不同。关键是,我们得到了一些奇怪的东西,例如,在 3 进数中,无限字符串 ...222222(左边是无限的!多么令人兴奋!)是数字 -1 的表示形式,无限字符串 ...11111112 表示 1/2,以及其他奇怪的乐趣。在弄清楚如何以 p 进数表示所有有理数以及如何使用它们进行算术运算之后,我们发现缺少了一些东西。
使用数字之间的常用距离,我们也会觉得有理数是不完备的。我们可以想到一些有理数序列,当它们平方时,会越来越接近 2,但是没有哪个有理数的平方是 2。我们可以找到一些有理数,它们越来越接近直径为 1 的圆的周长,但是数字 π 不是有理数。我们可以把实数看作当我们加入某些有理数序列(称为柯西序列)的极限,但最终并没有得到有理数本身时所得到的东西。这种技术的术语是完备化。实数集是有理数的完备化。我们可以对 p 进距离函数做同样的事情。存在一些有理数序列,它们在 p 进世界中并不会最终收敛到一个有理数。我们可以加入“缺失的”数字,以获得完整的 p 进数集。
你现在可能会有一个问题:“我为什么要这样做?!”构造 p 进数并非易事或直观。我听过一些拥有数学博士学位的人说,如果他们遇到 p 进数,他们总是不得不去查阅它的定义。我就是这样。肯定会有一些回报!
这个问题非常合理,是的,p 进数确实有很好的回报。首先,它们让我在 Twitter 上开了这个玩笑
有理数的最佳完备化,排名
10. 你
9. 不能
8. 排名
7. 它们
6. 它们是
5. 全部
4. 有用的
3. 并且
2. 美丽的
1. 实数
— Evelyn Lamb (@evelynjlamb) 2018 年 8 月 27 日
(有理数的完备化有无限多个,但它们只有两种类型:实数和所有素数 p 的 p 进数。我非常喜欢 p 进数,但思考 p 进数就像拼命地游泳。在进行完 p 进数锻炼后,能沉浸在温暖平静的实数浴缸中是一种解脱。不过,有些数学家不同意这种观点。在《Quanta Magazine》的一篇文章中,引用了 Scholze 的话,他说:“现在我发现实数比 p 进数要困惑得多。我已经习惯了它们,现在实数感觉非常奇怪。”)
p 进数不仅仅是用来在 Twitter 梗上晚到几个月。其中一个最重要的应用是解决我在文章开头提到的问题:确定特定方程是否有有理数解。如果一个多项式方程在考虑实数时有有理数解,那么它对于所有数字 p 也都有 p 进数解。这意味着如果你找到一个方程没有 p 进数解的 p,你就自动排除了有理数解。因此,如果可以通过某些 p 的 p 进数来轻松处理某个特定方程,那你可能很幸运。但是,总的来说,你可以用 p 进数代替实数做任何你想要的数字方面的事情,然后看看会发生什么。你可以使用 p 进数构建微积分的版本。你可以使用 p 进数构建复杂的代数和几何结构。p 进数是 Scholze 开创性工作的重要组成部分“完美空间”的根源。一些研究人员正在研究 p 进数是否能在物理学中产生成果。
阅读更多我喜欢的空间: 康托尔集 胖康托尔集 拓扑学家的正弦曲线 康托尔的漏帐篷 无限耳环 两条原点的直线 有两个房间的房子 法诺平面 环面 三维环面 莫比乌斯带 长直线 空间填充曲线 沃利斯筛子 沿着一条缝粘合的两个环面 空集 门格海绵 四个霍普夫链环的连通和 波罗密环 谢尔宾斯基三角形 单位正方形上的字典序 SNCF 度量 曼德勃罗集 法图煎饼 伪球面 杜阿迪兔子 庞加莱同调球面 科瓦列夫斯卡娅陀螺 一个 6 孔环面 实射影平面 一维球面 尼斯湖水怪 科赫雪花 双圆柱体 悬链面 SO(3) 伪菱形二十面体 莫泽纺锤 阿涅西的女巫 安托万项链 n 个圆的束