本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点。
当我高中英语课学到转喻和提喻这两个词时,我被它们深深吸引了。(当然,并没有着迷到我能够始终记住哪个是哪个的地步。也许这篇文章会改变这一点。我现在有了一个方便的新助记符,虽然对其他人几乎没有帮助:转喻用于矩阵。)
提喻是一种修辞手法,用部分代表整体,反之亦然。“全体船员到甲板上”是一种提喻:这些手大概是连接在整个人身上的,除非你正在看一部关于船的恐怖电影。“芝加哥赢得了世界大赛”用一个更大的整体——一个城市——代替了一个部分——他们的棒球队之一——尽管看到芝加哥庆祝,也许整个城市真的都赢了。但话又说回来,芝加哥是一个包含许多除了人之外的东西的地方,而庆祝世界大赛的人,嗯,是人,所以我猜这仍然是提喻。
转喻是用一个相关的词代替另一个词。“香槟”用“起泡的”代替可能是转喻,但也可能是提喻,因为气泡是在香槟里。这一切都非常令人困惑。更重要的是,提喻是转喻的一种,所以用转喻这个词来表示所有这些更安全。(另一方面,用提喻来表示所有转喻是提喻,这非常诗意。)
关于支持科学新闻
如果您喜欢这篇文章,请考虑订阅来支持我们屡获殊荣的新闻报道。 通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。 暂时抛开词语用法的复杂性,我一直在思考矩阵的数学转喻。 当我在二月份写关于空间SO(3)时,我注意到矩阵是一个数字数组,这个描述极大地低估了它的效用。(这就像把塞雷娜·威廉姆斯描述为脊索动物门的一员:没错,但真的不是重点。)
没错:矩阵是一个数字数组。但正是你对这些数字所做的事情才让它变得特别。矩阵在数学中最常用于表示线性变换。我们大多数人在早期教育中就学习了简单的线性变换。方程y=4x就是线性变换的一个例子。它碰巧是一个输入一个数字x,输出另一个数字y的变换。线性变换必须保持加法和标量乘法:如果向输入添加某个东西,则输出应按比例变化;如果将输入乘以某个特定量,则输出应乘以该量。
像y=4x这样的线性变换,那些输入一个变量并输出一个变量的变换,坦率地说,有点无聊。它们看起来都和y=4x一样,除了4的位置可能有一个不同的数字。(4 只是我选择的一个随机数。)但是线性变换可以输入比一个变量多得多的变量,并输出多得多的变量。
例如,假设我们要定义一个输入两个变量并输出两个变量的变换。假设我们想要输入坐标(x,y)并得到数字(2x+y,x+y)。我们可以用类似的方式定义许多不同的函数。存在将(x,y)转换为(5x-3y,πx+y)的函数,将(x,y)转换为(.3x,2y)的函数,以及大量的其他函数。数学家们开发了矩阵来处理这些函数。第一个函数可以用矩阵
表示,下一个用矩阵
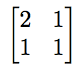
表示,下一个用
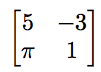
表示。
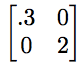
我们可以用它们来表示输入和输出变量数量不同的函数。将(x,y,z)转换为(z-y,x+2y)的函数得到矩阵
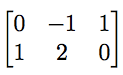
熟悉将矩阵应用于向量需要一些练习,而熟悉矩阵相乘来表示函数的组合(先执行一个函数,然后在第一个函数的输出上执行另一个函数)则需要更多练习,但一旦你做到了,它就是一个强大的工具。
作为一种工具,矩阵非常强大,以至于很容易忘记它是函数的表示,而不是函数本身。矩阵确实只是数字数组,但我想在这种情况下,大多数数学家都是转喻主义者。(转喻者?转喻主义者?)我们认为矩阵是函数本身,很容易忽略它只是一个符号。矩阵甚至不必编码线性变换。它们也在数学的其他领域中使用,将我们的定义限制为线性变换可能会忽略其他应用(尽管在我看来,矩阵作为一种表示线性变换的方式的价值远远超过它们的任何其他用途)。
在发布关于矩阵就像塞雷娜·威廉姆斯的推文后,我很高兴在 Twitter 上就矩阵、线性变换和线性代数的教学展开了热烈的讨论。有些人很高兴他们将线性变换与矩阵分开学习,有些人则很享受最终理解他们一直在努力的矩阵是更大的图景的一部分的“顿悟”。我认为在某个时候,人们必须进行一定程度的转喻才能达到他们可以舒适地使用矩阵作为线性变换并在该上下文中释放其全部能力的地步,但我们偶尔记住矩阵是转喻可能是好事。
