本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
上个月,我写了一篇关于围绕着一篇关于备受研究的普林顿 322 号泥板的新论文的炒作。这块古老的 Mesopotamian 泥板,在过去的几十年里一直是许多学术论文的主题,上面有与直角三角形相关的数字列,但我们并不确切知道该表格是如何或为何创建的。
在我的文章中,我批评了研究人员为配合论文发布而制作的宣传视频。具体来说,我对其中一位研究人员就 60 进制(或六十进制)与我们今天使用的 10 进制(或十进制)系统的相对效用所做的奇怪评论感到恼火。
需要明确的是,60 进制比 10 进制有一个很大的优势:60 可以被 3 整除,而 10 不能。用 10 进制很容易写出分数 1/2、1/4 和 1/5:它们分别是 0.5、0.25 和 0.2。但 1/3 是 0.3333…。它的十进制表示形式不会终止。这对我们来说真的不是什么大问题,因为我们习惯于将数字表示为小数或分数。但是巴比伦数字系统并没有像我们那样用分子和分母来表示分数。他们只使用六十进制形式,这就像我们只使用小数而不是将数字写成分数一样。在六十进制中,1/3 可以很容易地表示为。它是 20/60,在六十进制系统中可以写成 .20。(古代 Mesopotamian 人并没有完全那样写,因为他们没有相当于小数点的东西。我们稍后会回到这一点。)
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
当涉及到使用像 10 进制或 60 进制这样的位置数字系统轻松表示数字时,素数因子越多越好,但这些额外的因子是有代价的。在 10 进制中,我们只需要学习 10 个数字。30 进制(可以被 2、3 和 5 整除的最小进制,60 进制有一个额外的因子 2,这对于表示数字的容易程度来说并没有太大的区别)需要 30 个不同的数字。如果我们想用类似的表示形式来写像 1/7 这样的分数,我们就必须一直跳到 210 进制。使用如此多的数字很快就会变得很麻烦。
分母只有 2 和 5 因子的分数具有有限的十进制表示形式。12 进制也相当方便。它有 2 和 3 的素数因子,而且用一只手的指关节而不是单独的手指很容易数到 12。(我的一个数学史学生写了一篇帖子,主张使用 12 进制或十二进制数字系统。)使用 12 进制,我们将失去轻松表示 1/5 或 1/10 的能力。但是 30 或 60,允许素数因子 2、3 和 5 的最小进制,都非常大。这是一个权衡。就我个人而言,即使巴比伦数字那样相当不言自明,但要记住 30 或 60 个不同的数字对我来说也太多了,所以我坚持使用 10 或 12 进制。但是,如果那是你的菜,那就继续使用六十进制吧。
60 进制当然比 10 进制有主要的优势,但我对 Mansfield 在他们为配合论文制作的宣传视频中夸大这种优势的方式感到恼火。以下是我上个月写的关于它的内容
不同类型的三角函数表的效用可能是一个见仁见智的问题,但 UNSW 的视频也有一些关于 60 进制与我们现在使用的 10 进制系统中的准确性的彻头彻尾的谎言。在大约 1:10 处,Mansfield 说,“我们用 10 进制计数,它只有两个精确的分数:1/2,即 0.5,和 1/5。”我的第一个异议是任何分数都是精确的。数字 1/3 正好是 1/3。Mansfield 明确表示,他所说的 1/3 不是精确分数的意思是,它有一个无限(0.333…)而不是终止的小数。但是 1/4 呢?那是 0.25,它会终止,但 Mansfield 并不认为它是精确的分数。那么 1/10 或 2/5 呢?这些可以写成 0.1 和 0.4,这看起来相当精确。
令人难以辩解的是,当他赞扬 60 进制中可用的许多“精确分数”时,他并没有应用相同的标准。在 60 进制中,1/8 将写成 7/60+30/3600,这与在 10 进制中将 0.25 或 2/10+5/100 写成 1/4 的想法相同。为什么 1/8 在 60 进制中是精确的,而 1/4 在 10 进制中不是精确的?
我不想在这里重复我的文章,但我想澄清一点。一些批评这段视频批评的人认为,我在那里提到的数字只是视频中漂浮在空中的随机数字。它们不是!因为 Mansfield 没有解释这些数字的含义,所以它们可能看起来是随机的,但实际上,表达式 1/8=7.30 确实意味着一些东西。当我教数学史时,我让我的学生稍微使用了 60 进制算术,所以我立即认出了他展示的成对数字是 60 进制中的“倒数对”。对于公元前 1800 年受过数学教育的人来说,方程 1/8=7.30 的楔形文字等价物是有意义的。
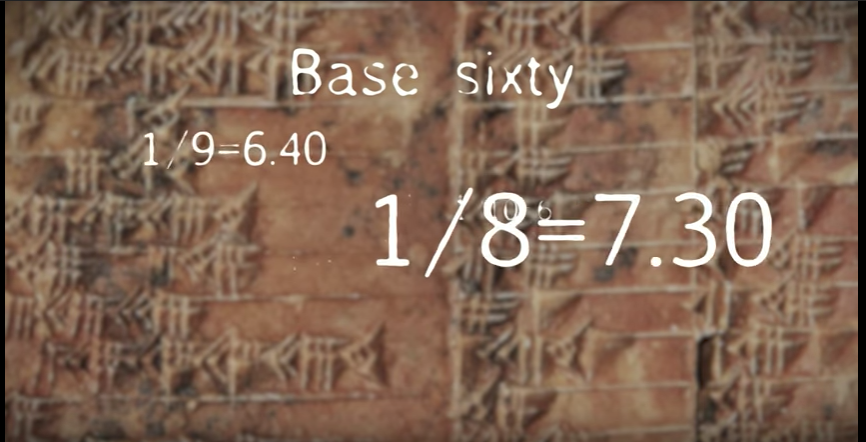
来自研究人员制作的宣传视频的截图,该视频是为了配合他们关于巴比伦泥板普林顿 322 的论文而制作的。 来源:UNSW
巴比伦数字系统是一种位置或位值系统,就像我们的系统一样。在我们的十进制系统中,数字 1 如果单独存在,可以表示一个单位,如果它在像 10 或 12 这样的数字的十位,则表示十,如果它在左边的下一个位置,则表示一百,依此类推。在位置 60 进制系统中,会有个位、六十位、三千六百位等等,而不是我们习惯的个位、十位和百位。但除此之外,该系统的工作方式与我们的系统相同。这与例如罗马数字形成对比,其中 I 表示一,X 表示十,C 表示一百,依此类推。因此,巴比伦系统比罗马系统更容易让我们使用。
但有一个转折:巴比伦系统did不使用零,至少在开始时是这样。(当 我在 2014 年开始教数学史时,我写了关于这个怪癖的文章。)我们使用零作为占位符,无论是在数字中间(如数字 101 中),还是在开头 (0.001) 或结尾 (1,000) 以指示我们正在谈论的数字的数量级。古代 Mesopotamian 人没有这样做,尽管他们确实在数字中间留出了一点空间用于空位,我们会在 101 中写零。他们假设上下文会使数量级清晰。在我们的数字系统中,这将类似于写 1 并假设它会清楚地表明是指一、十、十分之一、一百还是另一个我们只使用数字一和零来写的数字。
这听起来令人困惑,它确实导致了一些错误,但我们也基于我们书写数字的方式犯一些愚蠢的错误:例如,在某些人的笔迹中,数字 6 和 0,或 1 和 7 看起来很相似。如果上下文理解,我们有时甚至会省略数量级。人们谈论吃含有 100 卡路里的东西,这实际上意味着 100 千卡路里。房地产广告有时会说“100 美元起”的房屋(当我是个孩子时在德克萨斯州郊区)或“500 美元起”的单元房(在今天的大城市)。如果你带着几百美元出现,认为你会成为房主,你肯定会因为不理解这些数字末尾隐含的“千”而感到非常遗憾。
今天,计算机通常使用浮点运算来表示和操作数字,这可能会让你想起科学计数法。一组数字表示数字中的数字,另一组数字表示其数量级。这样,存储数字 12 和数字 12,000,000 基本上需要相同的内存量。尽管巴比伦系统没有像现代计算机那样清楚地指示数量级,但相似之处足以让一些人将其称为六十进制浮点。
在巴比伦数字系统中,1 可以表示一、六十、三千六百或其他 60 的幂,这一事实导致了一种不同的除法思维方式。如果他们不得不除以一个数字,他们会乘以该数字的“倒数”。如果两个数字的乘积是数字 1,则它们将互为倒数。但这可能意味着任何在 60 进制中写成数字 1 的等价物的东西:1、60、3600、1/60 等等。因此,4 和 15 在 60 进制中形成倒数对,因为 4×15 是 60。3 和 20、5 和 12 以及许多其他组合也是如此。(这些对可能感觉很熟悉:一刻钟有 15 分钟,三分之一有 20 分钟,等等。我喜欢将此视为残余的六十进制。)倒数表还包括更复杂的倒数对:8 和 7,30;9 和 6,40;1,21 和 44,26,40。(今天,当我们用我们的印度-阿拉伯十进制数字写六十进制数字时,我们通常在它们之间放逗号以避免歧义。7,30 表示一个位置是 7,一个位置是 30。数量级仍然取决于上下文。)
起初,像 1/4=15 和 1/8=7,30 这样的陈述对我和我的学生来说感到不自然,但我认为将它们转换回 10 进制可以有所帮助。当我还是个孩子的时候,我发现了一个惊人的事实:与其乘以 5(对我来说很困难),不如除以 2(对我来说很容易),然后再乘以 10。我并没有完全那样想。我更多地认为它是“除以 2,然后使数字大小合适”。后来我发现,人们可以逆转这个过程:你可以通过乘以 2 并使数字大小合适(通过除以 10,这看起来像是减去一个零或将小数点向左移动)来除以 5!我还发现,我可以通过使用相同的技巧并添加另一个 0 来乘以 50。
我对这些小技巧感到非常满意,但从未告诉我的老师,因为我确信我在作弊。如果被抓住,我就必须学习如何乘以或除以 5。太可怕了!我现在知道为什么我的技巧有效以及它们不是作弊。我正在使用 5 和 2 是十进制浮点倒数的事实。事实上,能够以方便的方式分解数字以使算术更容易是很好的。当我第一次接触巴比伦 60 进制系统时,我将 5-2 技巧识别为六十进制“倒数对”的 10 进制版本。虽然 Mesopotamian 数学可能不会改变我们进行三角运算的方式,但玩弄数字并了解不同的数字表示方式可以帮助学生(和非学生)发展我们的数字感并获得乐趣。
有关巴比伦数字系统的更多信息: 来自 MacTutor 数学史网站的巴比伦数字介绍 Duncan J. Melville 的 Mesopotamian 数学页面;特别参见“专题”,其中包括关于巴比伦倒数对的文章