本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
当你看着它时,它就静止不动,保持恒定。但如果你在康托集中的某个点上稍稍转过身,这个函数就会以令人难以置信的速度增长。

它不是哭泣天使,它是魔鬼的阶梯,或者,如果你不那么异想天开,就是康托函数。我第一次看到康托集被充分运用是在定义这个函数时,它是分析学或微积分学中常见的反例,而不是拓扑学。(如果你以前没见过康托集,请查看我上周关于它的帖子。)
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和思想的具有影响力的故事能够继续下去。
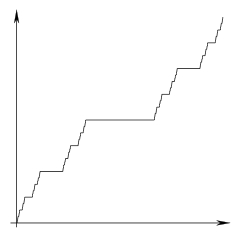
康托函数。图片来源:Theon,维基共享资源。CC BY-SA 3.0
就像康托集本身一样,有几种不同的方式来思考康托函数。第一种是像构建康托集一样,迭代地构建它。最终,我们希望在整个区间 [0,1] 上定义这个函数。我们将从构建康托集时移除的第一个区间开始,并声明函数在该区间上的值为 1/2。因此,如果 x 在 1/3 和 2/3 之间,则 f(x)=1/2。接下来,我们将定义它在接下来移除的两个区间上的行为。我们将区间 (1/9,2/9) 发送到 1/4,将 (7/9,8/9) 发送到 3/4。我们继续遵循这种模式:每个为构成康托集而移除的区间都会被发送到某个分母为 2 的幂的分数。其余的点只是“填补空白”。
这个动图很好地展示了这个过程。
如果你愿意用不同的进制来思考,还有另一种非常巧妙的方式来描述康托函数。首先,像描述康托集一样,你用 3 进制表示 0 到 1 之间的所有数字。如果一个数字包含 1,则在第一个 1 处截断它,或者等效地,用 0 替换所有后续数字。如果数字不包含 1,则暂时保持不变。无论哪种方式,下一步都是将数字中的所有 2 替换为 1,并以 2 进制而不是 3 进制解释结果。例如,数字 1/2 在 3 进制中写为 0.111...。我们在第一个 1 处截断它得到 0.1 或 0.100...,然后我们以 2 进制解释该数字。结果我们再次得到 1/2。
如果你记得康托集是可以以不含 1 的 3 进制书写的数字集合,那么有和没有 1 的数字应该区别对待似乎是合理的。当我们从第一个 1 处截断时,我们确保函数对于 1/3 和 2/3 之间的每个数字都取相同的值,这是我们在迭代构建康托集时移除的第一个区间。
当我们定义康托集本身时,我们必须小心以 1 结尾的有理数。令人惊讶的是,对于康托函数,我们不必小心!以 1 结尾的有理数可以重写为以无限个 2 结尾:1/3,或 0.1,与 0.02222… 相同,等等。(如果这看起来很奇怪,请记住 0.9999…=1。3 进制中的数字 2 的作用类似于 10 进制中的数字 9。)
你可能会认为这种歧义会成为一个问题,因为康托函数在某一点的值取决于该点是否包含 1。让我们看看 1/3,即 0.1 或 0.02222…。如果我们把这个数字看作 0.1,康托函数的定义告诉我们函数值应该是 0.1 (2 进制),或 1/2。如果我们把这个数字看作 0.02222…,我们应该把所有的 2 都改成 1,得到 0.01111…。当我们以 2 进制解释这个数字时,我们也得到 1/2。这在一般情况下都适用。所以我们可以用任何我们想要的方式写出康托集的端点,并得到相同的数字。
该函数在任何地方都是连续的,这意味着它在整个区间 [0,1] 上都有定义,并且不会跳跃。(我通常通过说一个函数是连续的,如果你可以在不将笔从纸上抬起的情况下绘制其图形,来直观地描述连续性,但如果我们考虑迭代地构建这个函数,这就不太好用了。)连续性并不太神奇。导数才是事情变得有趣的地方,康托函数成为了一个很好的反例。
在微积分中,一个函数在特定点是可微的,或具有导数,如果你可以在该点为其图形绘制切线。如果你学过微积分,你可能还记得你的老师对微积分基本定理的美妙之处感到有点陶醉。(或者只是我?)该定理表明,在某些条件下,求曲线下面积(积分)和求曲线斜率(微分)是“逆”运算。具体来说,微积分基本定理的一部分指出,对于“足够好”的函数,函数导数的积分告诉你函数在两个端点的值之差。
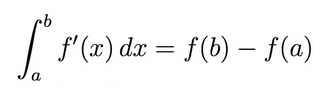
康托函数帮助我们理解“足够好”意味着什么。
在康托集之外的每个点,康托函数都是平坦的,因此很容易在该点为图形绘制切线。(那里的导数为 0。)正如我们上周看到的那样,康托集之外的点集总长度为 1,因此从技术意义上讲,该函数的导数“几乎处处”为 0。用哭泣天使的比喻来说,这意味着如果我们碰巧在任何时间点看它一眼,它很可能完全静止不动,因为我们可能会选择一个不在康托集中的点。在康托集的点上,情况就不同了。表现最好的康托集点具有“无限”导数,或垂直切线。更病态的点甚至没有这个。(有关康托函数究竟有多不可微的更技术性讨论,请查看这篇Richard Darst 于 1993 年发表的论文 (pdf)。)
在数学中,“几乎处处”对于很多事情来说都足够好了。人们可能会很自然地认为,如果一个函数在任何地方都是连续的,并且几乎处处可微,那么它应该足够好,以至于函数导数的积分可以告诉我们一些关于函数本身的有意义的信息。但是康托函数向我们表明,这些标准是不充分的。导数几乎处处为 0,因此导数的积分也是 0,但起始值为 0,结束值为 1。在我们没注意的时候,它悄悄地上升了。

