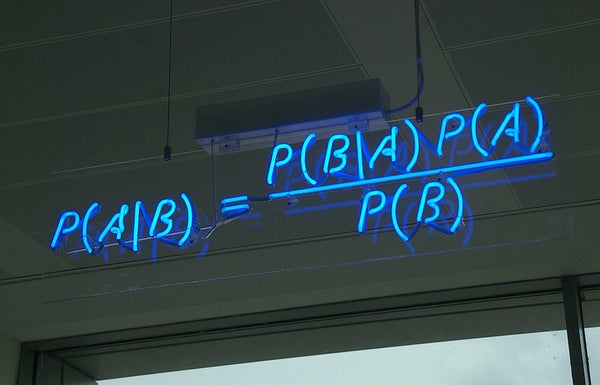本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在我们最近一期的播客“我最喜欢的定理”中,我的联合主持人凯文·努森和我与苏菲·卡尔进行了交谈,她是一位顾问,正如她所描述的那样,“在数字中寻找模式”。她也是大型互联网数学竞赛评选出的“世界上最有趣的数学家”,这是一个由 Aperiodical 在去年夏天主办的有趣比赛。(今年一月,我们邀请了2018年“世界上最有趣的数学家”尼拉·张伯伦作为节目的嘉宾。)
您可以在这里收听,也可以访问kpknudson.com,那里也有文字稿。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将有助于确保未来能够继续讲述关于发现和塑造我们当今世界的想法的具有影响力的故事。
我很高兴听到卡尔最喜欢的定理是贝叶斯定理,因为我一直觉得我对这个定理的理解不够深入。贝叶斯定理是关于条件概率的陈述——在已知其他条件的情况下,事件发生的概率。一个经典例子是,假设您的检测结果呈阳性,那么您患有该疾病的概率。答案取决于该疾病在人群中的流行程度以及检测的准确性——也就是说,如果您患有该疾病,检测结果呈阳性的可能性有多大,以及如果您没有患病,检测结果呈阳性的可能性有多大。如果一种疾病很罕见,并且该检测会将大量健康人误诊为患有该疾病,那么即使您的检测结果呈阳性,您也可能不太可能患有该疾病。
贝叶斯定理量化了这些概率。它也构成了贝叶斯统计的基础,贝叶斯统计是统计学的两个主要分支之一。(另一个是频率主义。)对贝叶斯统计和频率主义统计的复杂性和相对优点的完整解释比我想在这里讨论的要复杂得多,但它们来自关于概率和不确定性含义的两种不同哲学,统计学家可以使用这两种方法来开发帮助使用这些技术的人理解世界的技术。对于卡尔来说,贝叶斯定理和贝叶斯推断感觉像是人类通过与世界互动来学习的直觉方式的自然延伸。在贝叶斯推断中,您不断根据先前的信念和新的证据更新您的信念,使用诸如贝叶斯定理之类的工具。
在与卡尔讨论了贝叶斯定理之后,我仍然对贝叶斯定理的热情不高,但这一集确实帮助我更新了我的先验。再多一些积极的体验,我也可能成为贝叶斯爱好者。