本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点
注意:巧合的是,这篇文章发表后不久,就传出了关于 Facebook 令人不安的、可能非法的做法的新闻,即允许企业根据“种族亲和力”将用户排除在某些广告之外。我很乐意您阅读我这篇关于使用 Facebook 玩转拉姆齐理论的愚蠢博文,但如果您今天只打算阅读一篇与 Facebook 相关的文章,那么Pro Publica 揭露这种令人震惊的做法的文章 绝对更重要。
几乎每天早上,我都会查看 Facebook,看看我的哪些朋友在庆祝生日。我很少在网上祝他们生日快乐,因为这似乎太没有人情味了。(具有讽刺意味的是,在 Facebook 上收到这么多朋友的生日祝福总是让我感觉很棒,即使是那些我不常联系的朋友也是如此。我是否自相矛盾?好吧,那我就是自相矛盾。我很大,我包含了很多。)但我喜欢以一点拉姆齐理论开始我的一天:如果所有同一天生日的朋友都互相认识,或者他们都不认识彼此,我会感到兴奋。
拉姆齐理论在维基百科上的定义晦涩难懂,是“数学的一个分支,研究秩序必须出现的条件”。这相当有诗意,而且我认为如果你已经知道拉姆齐理论是什么,这似乎是一个很好的定义。但也许一个例子会更清楚地说明“秩序必须出现的条件”是什么意思。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将有助于确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
拉姆齐理论的常用例子通常被称为朋友与陌生人定理,这也是我进行 Facebook 生日检查的灵感来源:如果一个聚会上至少有六个人,那么一定有一组三个人都互相认识,或者三个人都是陌生人。数学家西蒙·潘佩纳在 Numberphile 上对此进行了解释,如果您想了解更多关于为什么这是真的的细节。另一方面,如果你的聚会上只有五个人,你就不能保证这一点。这个红色五边形内的蓝色星星就是证明。
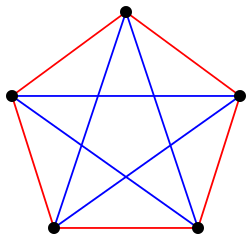
假设五边形的顶点是聚会上的五个人,如果他们互相认识,则用蓝线连接,如果他们是陌生人,则用红线连接。我们可以看到,每个三角形要么有两条红色边和一条蓝色边,要么有两条蓝色边和一条红色边。
来源:Richtom80 Wikimedia (CC BY-SA 3.0)
朋友与陌生人定理与必须出现的秩序有什么关系?这里的秩序是三个都互相认识或都是陌生人的人,而“必须出现”是指聚会上的人数达到六个时,朋友或陌生人的三角形是强制性的。
研究拉姆齐理论的人会说,拉姆齐数 R(3,3)=6。拉姆齐数 R(m,n) 是你必须邀请参加聚会的最小人数,以保证m 个人都互相认识或 n 个人都是陌生人。(数字 m 和 n 不必相同。)如果你想确保你能找到 3 个共同的朋友或 4 个共同的陌生人,你将要求拉姆齐数 R(3,4),它恰好是 9。
我的早晨 Facebook 仪式让我思考,关于我的 Facebook 好友,我可以提出哪些有趣的拉姆齐理论问题。生日这件事为正常的拉姆齐数问题增加了一层额外的结构。现在,我不再将我所有的朋友视为一个大群体,而是将他们分成 366 个较小的群体,每个群体对应一个可能的生日。(是的,我有闰日出生的朋友。)我好奇的问题是,是否需要任何相同颜色的节点成为一个互相认识的朋友或互相陌生的陌生人群体。我知道这对于我的个人朋友群体来说是正确的,但对于任何拥有与我相同数量的朋友的人来说,这是否也必须是正确的?或者更具体地说,我知道我一年中有几天有六个朋友是互相认识的朋友或互相陌生的陌生人。对于任何拥有与我相同数量的 Facebook 好友的人来说,这是否是必要的?为了使这种情况必须成立,最少需要多少 Facebook 好友?
当我思考了一段时间后,我意识到生日分组是一个转移注意力的东西。一年中的任何一天都可能在 0 到我所有朋友的生日之间。对于我的一些问题,你必须查看生日都在同一天的边缘情况,而对于另一些问题,你必须查看生日最大程度分散的边缘情况。无论哪种方式,你都不会得到比不按生日分组的问题更有趣或更困难的问题。好吧,有得必有失。
重点是什么?不仅仅是为了向你抛出一些拉姆齐理论的趣闻,虽然我确实喜欢这些趣闻。我只是想分享一种小方法,即一点数学在一定程度上丰富了我的生活。关于数学,特别是数学教育的讨论很多,都集中在为什么数学对工作或日常生活有用。我们也看到了相当多的关于数学之美的神秘主义。这些都很好,但我只是喜欢把数学作为另一种看待世界的视角。我略微了解拉姆齐理论的事实意味着,大多数早晨(有些日子我的 Facebook 朋友都没有生日),当我查看那里是否有有趣的朋友或陌生人配置时,我会多花几秒钟思考一些过生日的朋友。到目前为止,我注意到的最大的有趣群体是我认识的 3 月 5 日出生的六个互相陌生的陌生人。我正在祈祷有一天我能达到七个!