本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
上个月,我得知印度数学家Sharadchandra Shankar Shrikhande去世,享年102岁。这个名字听起来很耳熟,因为不久前我了解了“格雷科-拉丁方阵”,这是他最著名的数学构造。
要理解Shrikhande的工作,我们必须追溯到几个世纪前,传奇瑞士数学家莱昂哈德·欧拉(Leonhard Euler,1707-1783),他在去世前不久写到了这个问题。(这是他关于此论文的英文翻译。)拉丁方阵是一个n×n数组中n个符号的排列,使得每个符号在每行每列中出现一次。(数独是9×9的拉丁方阵,但也满足额外的要求。)顺便提一下,尽管名称是欧洲的,但在欧拉发现拉丁方阵之前,就已经有人研究过它们,包括韩国数学家崔锡鼎,他比欧拉早出生约70年。

一个4阶拉丁方阵。每个符号在每行每列中恰好出现一次。来源:Alejandro Vera Temiño Wikimedia (CC BY-SA 3.0)
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
作为一点澄清,虽然欧拉的论文被称为“关于一种新型幻方的研究”,但今天大多数数学爱好者不会称它们为幻方。一个n×n阶的幻方使用1到n2之间的每个数字恰好一次,而拉丁方阵仅使用1到n之间的数字,但每个数字使用n次。
格雷科-拉丁方阵是一个n×n数组中两组n个符号的排列,使得每组符号形成一个拉丁方阵,并且没有一对符号出现两次。这个名称可以使其更容易想象:第一组符号可以是拉丁字母表的前n个字母,第二组可以是希腊字母表的前n个字母。每个可能的拉丁字母和一个希腊字母的组合必须在格雷科-拉丁方阵中恰好出现一次。数字n是格雷科-拉丁方阵的阶数。
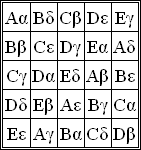
一个使用希腊字母和拉丁字母前五个字母的5×5格雷科-拉丁方阵。拉丁字母形成一个拉丁方阵,希腊字母也是如此,并且每个拉丁字母和一个希腊字母的组合都恰好出现一次。来源:Maksim Wikimedia
欧拉的研究使他得出结论,格雷科-拉丁方阵存在于奇数阶和4的倍数阶。不存在2阶格雷科-拉丁方阵(您可以自己检查),欧拉试图构造一个6阶的,但没有成功,这使他推测不存在4n+2阶的格雷科-拉丁方阵。关于不存在6阶这种方阵的严格证明花了一些时间。(丹麦数学家托马斯·克劳森声称他在1842年的一封信中证明了这一点,但该证明已遗失。 加斯顿·塔里在1901年给出的证明是最早仍然存在的。)
研究人员开发了基于较小阶方阵构造某些阶格雷科-拉丁方阵的方法。例如,一个4阶格雷科-拉丁方阵和一个3阶格雷科-拉丁方阵可以组合形成一个12阶格雷科-拉丁方阵。但他们的技术不适用于恰好有一个因子为2的阶数,如2、6和10,因此他们没有解决形式为4n+2的较大数字的问题。
最后,在1959年,Shrikhande、Raj Chandra Bose和Ernest Tilden Parker破解了这个密码,发表了几篇论文,完全解决了这个猜想,不仅证明了10、14、18等阶的格雷科-拉丁方阵存在,而且还构造了某些维度的格雷科-拉丁方阵。他们赢得了“欧拉的破坏者”的绰号。(为了使其有效,你需要知道欧拉的发音像“oiler”,而不是“yooler”。)这篇文章顶部的图片是一个彩色的10阶格雷科-拉丁方阵的例子。
格雷科-拉丁方阵主要只是有趣,但它们在设计科学实验中也有一些令人惊讶的实际应用。多米尼克·克莱夫和李·斯坦科斯基撰写的一篇关于格雷科-拉丁方阵的论文指出,格雷科-拉丁方阵(以及更高阶的类似方阵,在数组中每个方框中不仅有两个,而且有三个或更多符号)可用于设置实验,在这些实验中,许多不同的测试对象需要比较他们在几个不同测试中的表现。查看克莱夫和斯坦科斯基的文章,了解更多关于从欧拉到猜想“破坏”后几十年问题历史的信息。要了解更多关于Shrikhande本人的信息,请阅读Nithyanand Rao的这篇文章,该文章是在Shrikhande 100岁生日之际撰写的。
