本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
猴子!数学群!四维几何!终于在一起了!
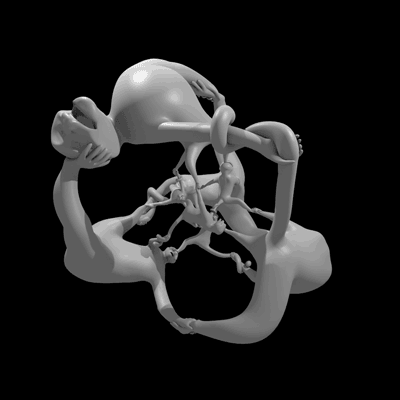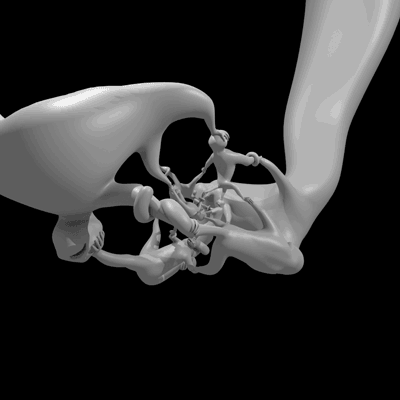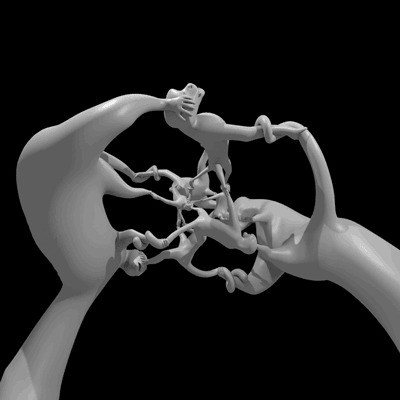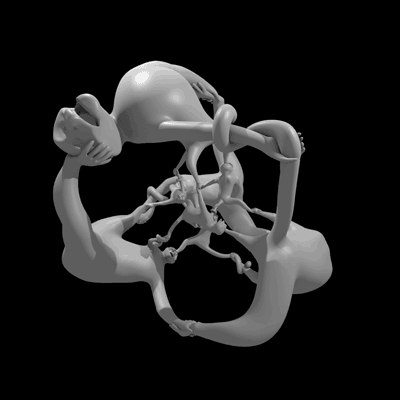
雕塑“猴子超立方体比什么都好玩”在四维空间中旋转的动画。(由于我们感知的限制,我们实际上是在观看四维物体的投影。)图片来源:亨利·塞格曼和威尔·塞格曼。
这个名为猴子超立方体比什么都好玩的雕塑,回答了一个悬而未决的问题:四元数群是否曾经作为某个物体的对称群出现过?感谢数学家亨利·塞格曼和数学音乐家维·哈特,现在的答案是肯定的。他们关于这个雕塑的非常易懂的论文将发表在2014年Bridges数学-艺术会议的会议记录中,您现在可以在预印本服务器arxiv上免费阅读。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
为了理解猴子的含义,我们需要谈谈群。数学中“群”的含义比英语中的含义更具体。最抽象地说,群是一组元素和一个运算,该运算接受集合中的两个元素并吐出第三个元素,并有一些额外的要求。例如,当您将两个整数相加时,您会得到一个整数。群还需要有一个单位元素,一个保持其他元素不变的元素。对于整数,0 扮演着这个角色。群需要有逆元素:每个元素都必须有一个逆元素,以便当您将它们配对时,您会得到单位元素。对于整数,我们有相反数:+1 和 -1,+2 和 -2,等等。最后,群需要具有结合律:如果您将三个整数相加,例如 1+2+3,那么您是先做 1+2(得到 3+3)还是先做 2+3(得到 1+5)都无关紧要。无论哪种方式,您最终都会得到 6。所有群都必须遵守该规则。但这些是唯一的规则,任何满足这些规则的元素集合和运算都是一个群。
群不必像整数那样是无限的。有限群的一个例子是数字1和-1与乘法运算。它只用两个元素就满足了所有规则。我们甚至可以从视觉上思考这个群,从变换的角度来看。元素1保持一切不变(它是单位元素),而-1则将事物沿一条线反射。如果您有一个具有双边对称性的物体,您可以将其沿对称线反射,物体看起来仍然相同。因此,-1变换代表了物体的对称性。

这张苹果的图片(大部分)在沿蓝线反射时保持不变。图片来源:伊芙琳·兰姆,基于 Rasback,通过维基共享资源 的照片。
如果双边对称性是图片或物体唯一的对称性,那么由1和-1以及乘法组成的群被称为其对称群。但是对于这张苹果的图片,我们也有旋转对称性。如果我们旋转 1/5 圈,图片仍然相同。让我们将该旋转命名为a。

这个苹果的对称性包括沿蓝线的反射和标记为“a”的旋转。图片来源:伊芙琳·兰姆,基于 Rasback,通过维基共享资源 的照片。
我们可以对图片执行旋转a最多 5 次,此时我们回到单位元素。我们还可以将这些旋转中的任何一个与-1反射结合起来。最后,这张苹果图片的对称群可以用元素1, -1, a, -a, a2, -a2, a3, -a3, a4, 和 -a4来表示。(您可以在维基百科的 二面体群 页面上阅读更多关于为什么这些是此对称群的唯一元素的信息。)
群和对称性之间的关系一直是研究具有对称性的物体和群本身的一种有用的方法。在他们的论文中,哈特和塞格曼提出了一些关于群和对称性的问题
“1. 哪些群可以表示为某些真实世界物理物体的对称群?
2. 哪些群实际上已被表示为某些真实世界物理物体的对称群?
3. 是否存在任何明显的差距——小的、美丽的群,它们应该在对称物体中具有物理表示,但到目前为止还没有?”
他们专注于问题#3:确实存在一个小的、美丽的群,即四元数群,到目前为止它还没有物理表示。它只有 8 个元素:1, -1, i, -i, j, -j, k, 和 -k。这是它的乘法表。(在这个群中,乘法顺序很重要,左边的元素在顶部的元素之前。所以 ij=k,但 ji=-k。)
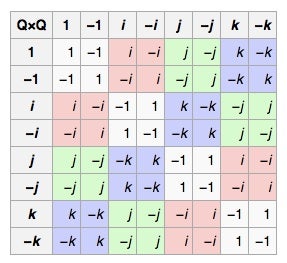
四元数群的乘法表。
数字 1 和 -1 的行为正常。数字 i、j 和 k 的平方都为 -1(所以它们有点像 虚数),并且 i、j 和 k 之间存在循环关系:ij=k,jk=i,ki=j。(如果您学过物理或多元微积分,这可能会让您想起叉积。)
四元数群尚未作为物理物体或艺术品的对称群出现的一个原因是,它不是平面或三维空间对称群的子群。换句话说,在二维或三维空间中,不存在任何旋转、平移和反射的组合,可以保持空间完整并具有四元数群的结构。
但是,由于哈特和塞格曼是富有创造力、意志坚定的人,他们并没有被像三维几何约束这样的小细节吓倒!四元数群是四维空间对称群的子群,所以他们做了合乎逻辑的事情,将维度提升了一维。塞格曼已经可视化四维物体投影一段时间了。(我在 2012 年写过关于它的文章。)如果您有一个三维物体,您可以将其二维可视化的方法之一是将光源对准它,并查看其在墙上的阴影。塞格曼和他的合作者使用了类似的技术,维度提升了一维,制作了四维物体投影的 3D 打印件。塞格曼在 YouTube 上发表了一个关于该技术的一小时演讲,他和索尔·施莱默在 这里 (pdf) 写了关于该技术的文章。
这个雕塑,除了上面的动画之外,还借助 3D 打印的魔力实现了物理实体,由塞格曼和他的兄弟威尔设计。他们从四维立方体的类比物开始,有时称为 超立方体、四方体或 8-胞体。超立方体的对称群比四元数群更大,所以他们必须做一些事情来减少对称性的数量。这就是猴子出现的地方。为了减少对称性的总数,他们在超立方体的 8 个立方体中的每一个的中心放置了一只猴子。* 每只猴子都有两条胳膊、两条腿、一条尾巴和一个头。这使得只有少数几种方法可以扭转和转动物体,并且仍然保持猿类附肢的位置。通过正确的猴子方向,他们设法将对称性限制到足以获得四元数群。(有关完整详细信息,我敦促您阅读 该论文。)然后,就是使用塞格曼的投影技术使猴子成为现实的问题。就像在墙上制作皮影戏一样,投影会扭曲尺寸。因此,猴子在四维空间中尺寸相同,但它们在三维空间中的投影使其中一些看起来更大。
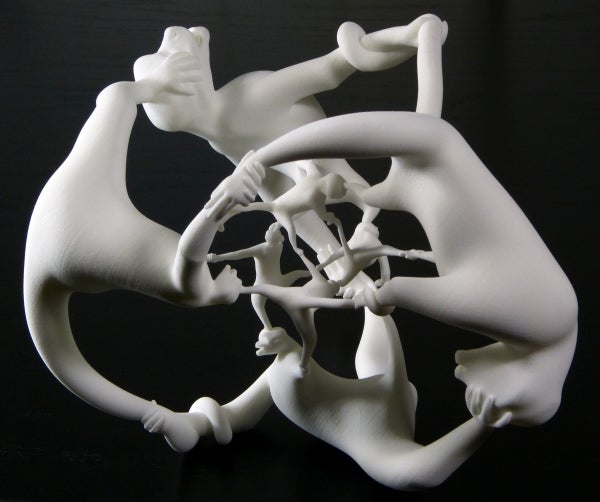
猴子超立方体比什么都好玩,一个具有四元数群对称性的雕塑。图片来源:亨利·塞格曼和威尔·塞格曼。
我希望哈特、塞格曼和塞格曼(以及其他数学艺术家)将继续将其他被忽视的群变成对称群。我希望能看到一个怪兽的怪兽群!
*更正:这句话最初声明在超立方体的每个顶点都有一只猴子。在超立方体的每个立方体中都有一只猴子。