本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在今天的播客“我最喜欢的定理”节目中,我的联合主持人凯文·克努森和我很高兴与悉尼大学的应用数学家纳莉妮·乔希交谈。(我们特别高兴能成为这一集的时间旅行者。凯文和我在星期四下午录制,而乔希博士在星期五早上加入了我们。)您可以在这里或 kpknudson.com 收听这一集,那里也有文字稿。
乔希博士选择与我们分享复分析中的米塔-列夫勒定理。如果您没有复分析的背景,这里的一些背景知识可能会帮助您理解本集中的主要思想。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保关于塑造我们今天世界的发现和想法的具有影响力的故事的未来。
复分析处理复平面上的函数。复平面上的点具有 x+iy 的形式,其中 x 和 y 是实数,i 是 -1 的平方根。但复平面的真正威力在于,通过将自然具有两个坐标的平面上的点视为单个数字,微积分变得更加强大。
我们也可以在复平面上定义所有正常的微积分内容。例如,导数,即函数在某一点的变化率,在复平面上是有意义的。但是,对于一个函数来说,在复平面上的某一点完全可微或解析,比函数在多元微积分意义上具有导数要困难得多。这忽略了很多内容,但主要的结论是,您可以将解析函数视为光滑的。
与处处解析的函数(也称为全纯函数)密切相关的是亚纯函数。这些函数在除称为极点的孤立点之外的所有地方都是解析的,在极点处,函数以某种受控的方式爆发。乔希博士用火山点缀景观的生动形象来描述亚纯函数。除了火山之外,景观是平滑而温和的。
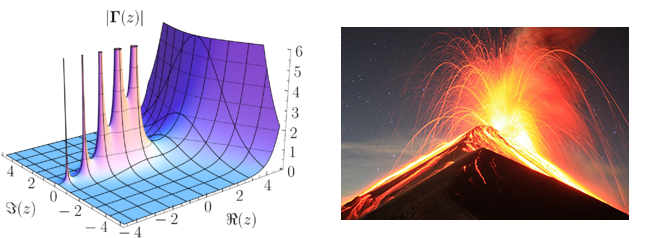
左图:亚纯函数的图。右图:危地马拉的富埃戈火山爆发。这两张图片几乎无法区分。图片来源:Geek3 维基共享资源(CC BY-SA 3.0)(左), Kevin.Sebold 维基共享资源(CC BY-SA 3.0)(右)
米塔-列夫勒定理,以瑞典数学家戈斯塔·米塔-列夫勒(Gösta Mittag-Leffler,1846-1927)的名字命名,涉及复杂的“法医分析”,这个术语是我刚刚编造的。它说,如果您知道极点的位置以及函数在极点周围的行为或用乔希博士的话说“强度”,您基本上可以重建一个亚纯函数。这些信息足以重建函数,至少在一定程度的摆动空间内。
我很惊讶一位应用数学家选择了一个似乎是纯粹的复分析定理,我认为复分析不是非常应用(尽管这可能仅仅是因为我个人与它的关系)。但乔希博士告诉我们米塔-列夫勒定理的宏大思想,即获取局部信息并将其转化为全局信息的思想,对她构建数学“工具箱”以帮助人们解决现实世界问题的工作非常重要。(如果您像我一样对她随意提及墨西哥库埃纳瓦卡公共汽车的数学感到好奇,请查看皮奥特·瓦尔乔夫的这篇 arxiv 论文。)
在播客的每一集中,我们都会要求我们的嘉宾将他们的定理与生活中的食物、饮料、艺术、音乐或其他乐趣搭配。乔希博士出生于缅甸,并选择了 htamin le thoke,一种混合了多种食材的缅甸米饭沙拉。像早期的嘉宾艾米·拉顿斯卡娅一样,她也建议史蒂夫·莱奇作为合适的音乐伴奏。您必须收听这一集才能了解le thoke 和莱奇为什么与米塔-列夫勒定理完美搭配。
您可以在她的网站、Twitter 或她的著作 离散系统与可积性 中找到乔希博士。有关米塔-列夫勒定理及其历史的更多信息,请查看劳拉·E·特纳在Historia Mathematica 上发表的 这篇文章。您可以在 kpknudson.com 和 Unity 之根 找到有关本播客中数学家和定理的更多信息,以及其他令人愉悦的数学佳肴。 文字稿可在此处获取。 您可以 在 iTunes 和其他播客交付系统上订阅和评论播客。 我们很乐意听到听众的来信,请发送邮件至 myfavoritetheorem@gmail.com。凯文·克努森在 Twitter 上的账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。请在下次加入我们,了解另一个引人入胜的数学知识。
“我最喜欢的定理”节目回顾
第 0 集:主持人最喜欢的定理 第 1 集:艾米·威尔金森最喜欢的定理 第 2 集:戴夫·里切森最喜欢的定理 第 3 集:艾米莉·戴维·劳伦斯最喜欢的定理 第 4 集:乔丹·艾伦伯格最喜欢的定理 第 5 集:杜莎·麦克达夫最喜欢的定理 第 6 集:海伦中荣最喜欢的定理 第 7 集:亨利·福勒最喜欢的定理 第 8 集:贾斯汀·柯里最喜欢的定理 第 9 集:艾米·拉顿斯卡娅最喜欢的定理 第 10 集:穆罕默德·奥马尔最喜欢的定理 第 11 集:珍妮·克莱兰最喜欢的定理 第 12 集:坎迪斯·普莱斯最喜欢的定理 第 13 集:帕特里克·霍纳最喜欢的定理 第 14 集:劳拉·塔尔曼最喜欢的定理 第 15 集:费德里科·阿迪拉最喜欢的定理 第 16 集:贾亚德夫·阿特雷亚最喜欢的定理
