本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
上个月,我写了一篇关于我每天早上在 Facebook 上玩的一个小数学游戏。我查看哪些朋友那天过生日,哪些朋友互相认识,哪些朋友互不相识。通常情况是两者兼有,但当只有其中一种情况时,我会感到兴奋。
与这种情况相关的数学分支称为拉姆齐理论。它处理许多不同的情况,在这些情况下,我们想要计数事物,并查看某些配置(即所有朋友或所有陌生人)是否必然出现。在上个月的文章中,我提到了拉姆齐数,它与派对上的共同朋友或陌生人有关。具体来说,拉姆齐数 R(m,n) 是你必须邀请参加派对的最小人数,以保证m 个人都互相认识,或者 n 个人都是陌生人。例如,如果你邀请六个人参加派对,你保证会得到一个由三个互相认识的朋友组成的小团体,或者一个由三个互相不认识的陌生人组成的群体,他们尴尬地盯着彼此在潘趣酒碗旁。所以 R(3,3)=6。
(朋友或陌生人的背景并非真正必要。我们可以将每个人想象成图中的一个点,如果两个人互相认识,则用蓝线连接,如果他们互不相识,则用红线连接。)
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
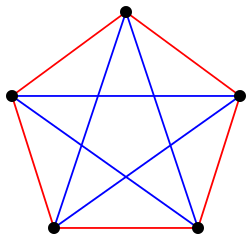
一个有五个人参加的派对中的社交关系图。两个人如果是朋友,则用蓝线连接,如果是陌生人,则用红线连接。这张图片证明 R(3,3) 必须大于 5,因为每个三角形都有两条蓝色边和一条红色边,或者两条红色边和一条蓝色边。
图片来源:Richtom80 Wikimedia (CC BY-SA 3.0)
我们对拉姆齐数的知识限制令人惊讶。我们知道 R(3,3)=6,但如果我们正在寻找一种方法来保证只有四个共同的朋友或陌生人,我们必须邀请 18 个人,这是一个相当大的跳跃。我们甚至不知道五个共同朋友或陌生人的答案。它介于 43 和 49 之间[更新:在 2017 年 3 月,Vigleik Angeltveit 和 Brendan D. McKay将 R(5,5) 的上限从 49 降低到 48],但我们尚未准确地确定它。
当我在研究我关于拉姆齐理论和 Facebook 的文章时,我看到了 这段引言,它来自 多产的数学家保罗·埃尔德什,出自罗纳德·格雷厄姆和乔尔·斯宾塞 1990 年在《大众科学》上发表的文章。
假设外星人入侵地球,并威胁说如果人类在一年内找不到红色五和蓝色五的拉姆齐数,就会将地球摧毁。我们可以召集世界上最聪明的人才和最快的计算机,并且在一年内我们可能会计算出这个值。然而,如果外星人要求红色六和蓝色六的拉姆齐数,我们将别无选择,只能发动先发制人的攻击。
换句话说,如果外星人正在寻找 R(5,5),我们会尝试计算出 R(5,5)。如果他们正在寻找 R(6,6),我们会尝试找出如何击败外星人。诚然,这是一个愚蠢的假设,但是什么时候阻止过任何人?
仅仅为了好玩,我决定进行一些粗略的计算,看看摩尔定律对计算机处理能力的影响可能对那句话产生什么影响。如果埃尔德什今天说这句话,他是否需要更改数字?将摩尔定律解释为自 1990 年以来计算速度每 18 个月翻一番,计算速度应该提高了约 217 倍,或 131,072 倍。这非常令人鼓舞。如果我们在 1990 年可以用一年时间计算出 R(5,5),那么今天只需要几分钟。(记住,这是假设我们使用了世界上所有最聪明的人才和最快的计算机。)
那么 R(6,6) 呢?它比 R(5,5) 困难多少?我们知道 R(5,5) 介于 43 和 49 之间。例如,一组 45 个人可能以许多不同的方式相互联系。45 个人之间共有 990 种成对关系,每种关系可能是友谊或陌生。那是 2990,大约是 10298,不同的朋友和陌生人配置,我们必须筛选这些配置,在每一种配置中寻找 5 个共同朋友或共同陌生人的集合。(作为参考,宇宙中大约有 1080 个原子。)
对于六个朋友或陌生人,我们遇到了更大的麻烦。我们知道 R(6,6) 介于 102 和 165 之间。在低端,有大约 101550 种可能性需要检查 102 个人。这比我们在 R(5,5) 中看到的可能性大约多 101250 倍,远远超过了我们从摩尔定律获得的 131,072 倍的加速因子。
现在,图的绝对数量并不是一切。有一些方法可以减少您必须检查的可能性数量。由于我不是拉姆齐理论家,我不知道所有这些方法,所以我不知道这个问题可以简化多少。我确信可能性的数量可以减少许多数量级, 但我愿意打赌,即使我们将计算速度提高 131,072 倍,101250 这个数字也代表着一个障碍,使得 R(6,6) 比 R(5,5) 难以逾越。
所以我的结论是,与找到 R(6,6) 的计算成本相比,摩尔定律只是沧海一粟。祝贺你,僵尸埃尔德什,你赢了这一轮!如果我们真的受到强大但又异常一心一意的外星人攻击, 他们的目的是摧毁地球,除非我们告诉他们 R(6,6),否则我们仍然必须与他们战斗。