本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在这一集“我最喜欢的定理”中,我的联合主持人凯文·努森和我很高兴与哈维·穆德学院的数学教授 Mohamed Omar 交谈。您可以在这里收听这一集,或者在 kpknudson.com 收听。
奥马尔博士最喜欢的定理是伯恩赛德引理。数学家通常使用“引理”这个词来表示一个较小的定理,或者是在证明一个更大的定理时使用的定理,但这个引理本身就是一个令人印象深刻的定理。(正如奥马尔博士指出的那样,这个定理甚至不是来自一位名叫伯恩赛德的数学家。因此,如果伯恩赛德部分不正确,那么引理部分也可能不正确,我们可以将其提升为定理的地位。)
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们今天世界的发现和想法的具有影响力的故事。
伯恩赛德引理 涉及组合数学和代数。组合数学基本上是计数。虽然这比用手指计数要难一点。您可能试图确定一副牌中可能有多少个满堂红,或者在棋盘上可以有多少种排列棋子的方式。代数通常是对数学对象集合中的对称性和关系的研究。因此,伯恩赛德引理解决了对象的对称性如何影响其组合数学。
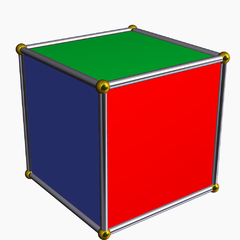
一个面被涂成红色、绿色和蓝色的立方体。伯恩赛德引理可以帮助您计算有多少种基本不同的方法来给面着色。图片来源:Stella Software,作者:Robert Webb Wikimedia
所有这些都有点抽象,但奥马尔博士给了我们一个非常具体的例子来思考。你从一个立方体开始,你可以给每个面涂上红色、绿色或蓝色。你可以用多少种不同的方法来给它着色?仅使用这些信息,每个面都有 3 种颜色选择,共有 6 个面,因此您得到 36 或 729 种可能的着色方式。但是,如果以这种方式计数,事情就会变得有点愚蠢。顶部面为红色而所有其他面为绿色的立方体与底部面为红色而所有其他面为绿色的立方体不同。但是,只需将其翻转过来,就可以轻松地将其中一个立方体变成另一个立方体。您可能希望将这两种着色方式视为相同,以及任何两种着色方式,对于这两种着色方式,您可以拿起其中一种并旋转它以获得另一种。
这就是伯恩赛德引理的用武之地。它允许您使用立方体的对称性集合(形成一个称为群的结构)来更准确地计算可能的着色方式。并且该引理不仅适用于立方体和着色。任何时候您研究具有某些对称性集合的对象的配置或构象(即使是非常抽象的对称性),您都可以使用伯恩赛德引理来计数它们。我们在播客中使用了一些代数术语。如果您想了解有关其中一些术语的更多信息,这里有一些链接:群(或 如果您喜欢诗歌形式的定义,请点击此处);轨道和稳定器;轨道-稳定器定理(适用于具有较强数学背景的人)。
在播客的每一集中,我们都会请嘉宾将他们的定理与某物配对:食物、饮料、音乐、文学或生活中的任何其他乐趣。奥马尔博士选择将伯恩赛德引理与棋盘大理石蛋糕搭配。您必须收听这一集才能找出为什么这与伯恩赛德引理完美搭配。
您可以在奥马尔博士的 网站、Twitter 或他的著作 《走向 RSA 密码学的数论》 中找到他。您可以在 kpknudson.com 和 Unity 之根 找到有关此播客中数学家和定理的更多信息,以及其他令人愉悦的数学知识。 此处提供文字稿。您可以在 iTunes 和其他播客分发系统上 订阅和评论播客。我们很乐意听到听众的来信,请发送邮件至 myfavoritetheorem@gmail.com 联系我们。凯文·努森在 Twitter 上的账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。下次加入我们,学习另一个引人入胜的数学知识。
之前在“我最喜欢的定理”节目中
第 0 集:主持人最喜欢的定理 第 1 集:Amie Wilkinson 最喜欢的定理 第 2 集:Dave Richeson 最喜欢的定理 第 3 集:Emille Davie Lawrence 最喜欢的定理 第 4 集:Jordan Ellenberg 最喜欢的定理 第 5 集:Dusa McDuff 最喜欢的定理 第 6 集:Eriko Hironaka 最喜欢的定理 第 7 集:Henry Fowler 最喜欢的定理 第 8 集:Justin Curry 最喜欢的定理 第 9 集:Ami Radunskaya 最喜欢的定理
