本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点。
与 π 和 e 一样,黄金比例 也是一个数字名人。它是一个非常特殊的矩形边长的比率。如果你取这个矩形,并从中切下尽可能大的正方形,你剩下的另一个矩形与第一个矩形具有完全相同的边长比率。这种构造定义了边长之间独特的关系,任何边长具有这种关系的矩形都称为黄金矩形。如果黄金矩形的短边长为 1,则长边长为 (1+√5)/2,约为 1.618。
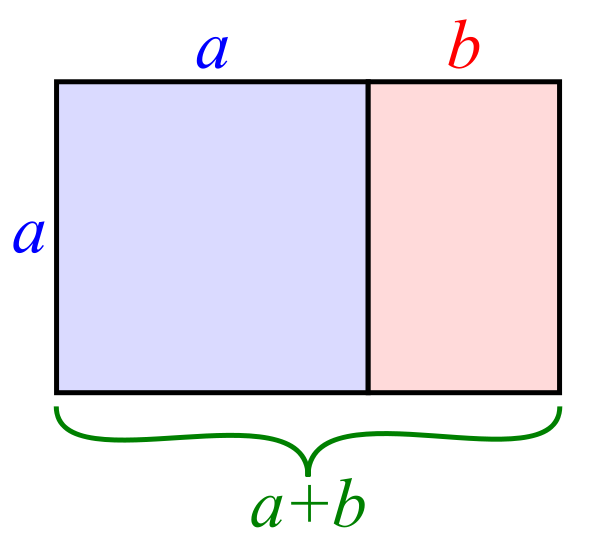
一个“黄金矩形”可以被切割成一个正方形和另一个黄金矩形。a+b 与 a 的比率与 a 与 b 的比率相同。
黄金比例对于许多数学爱好者来说都很熟悉,但你听说过白银比例吗?青铜比例呢?这些是其他类似构造的无理数,它们不如其华丽的黄金表亲那样广为人知。与黄金比例一样,每个所谓的金属平均数都可以被可视化为特殊矩形上的边长比率。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
对于白银比例,我们希望切掉两个正方形,并剩下一个与第一个矩形具有相同纵横比的矩形。
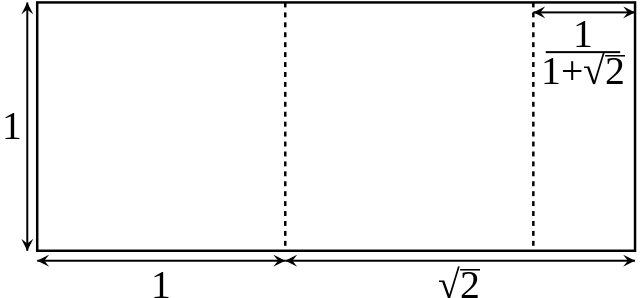
一个“白银矩形”可以被切割成两个正方形和另一个白银矩形。边长比率为 1+√2,约为 2.414。图片来源:Krishnavedala,来自维基共享资源。
对于青铜比例,我们希望切掉三个正方形,最终得到一个相似的矩形。
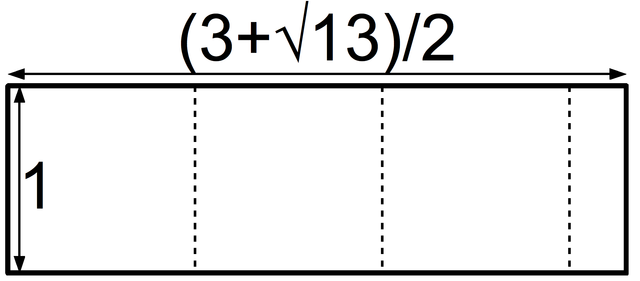
一个“青铜矩形”可以被切割成三个正方形和另一个青铜矩形。青铜比例为 (3+√13)/2,约为 3.303。图片来源:Hyacinth,来自维基共享资源。
除了黄金、白银和青铜之外,对于金属的珍贵程度或期望值并没有规范的排序,但我们可以继续创建这些比例。我们可以将下一个称为紫铜比例。“紫铜矩形”可以被切割成四个正方形和另一个紫铜矩形,紫铜比例将为 2+√5,或约 4.24。
随着我们不断前进,也许下一个是镍或铝,矩形会变得越来越长,因此不难看出,每个金属平均数都比上一个大,就像黄金比例介于 1 和 2 之间一样,白银比例介于 2 和 3 之间,青铜比例介于 3 和 4 之间,并且模式继续:第 n 个金属平均数始终介于整数 n 和 n+1 之间。
黄金比例与 著名的斐波那契数列 1、1、2、3、5…… 有着有趣的关系,其中每一项都是前两项之和。随着斐波那契数列的项数增加,相邻项之间的比率接近黄金比例。同样,其他金属平均数也与其他数列有这些关系。对于白银比例,它是佩尔数列。它从 0、1、2、5、12、29…… 开始。第 n 项是第 (n-2) 项和 2 倍的第 (n-1) 项之和。对于青铜平均数,公式中有 3 而不是 2,依此类推。
当我与威斯康星大学麦迪逊分校的应用数学家 Jean-Luc Thiffeault 谈论太妃糖拉伸机时,我了解了金属平均数。在他最近的一篇 论文 中,他对历史悠久的太妃糖拉伸机专利进行了数学分析,根据它们在每次通过拉伸机时拉伸糖果的程度对其进行分类。因此,如果你每次拉伸都将太妃糖的长度加倍,那么你的拉伸比率将为 2。他发现一些太妃糖拉伸机的拉伸比率基于黄金比例和白银比例。
你实际上可以在 1918 年的黄金比例太妃糖拉伸机专利中看到黄金比例与斐波那契数列之间的关系。齿轮的运动意味着手柄的每次转动基本上都会将前两个步骤加在一起。如果我们的原始太妃糖块(下图左上角)的长度为 1,则下一步的长度为 2。然后下一步的长度为 3,下一步为 5,依此类推。随着时间的推移,拉伸比率将趋向于黄金比例,我们可以看到斐波那契数列的步骤如何将我们带到那里。
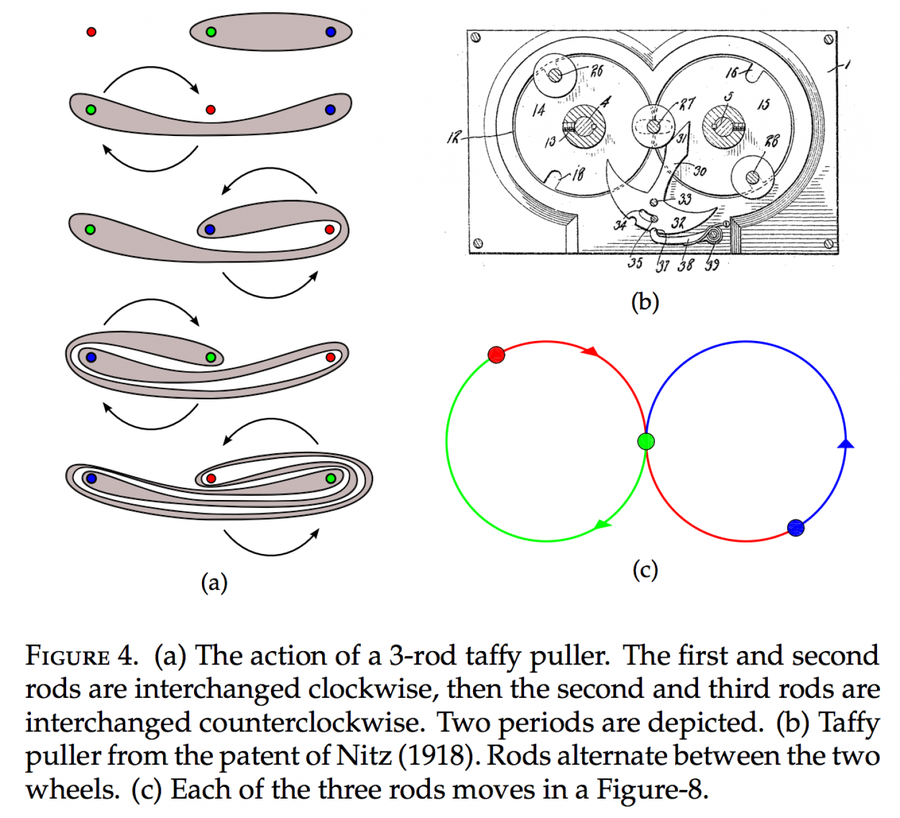
在 我在史密森尼网站上发表的文章 中阅读更多关于太妃糖拉伸的数学原理。
