本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
有一个老套的关于数学家的笑话(或者工程师,甚至是芬兰人),说如果你和一个数学家交谈时,他们看着你的鞋子,你就能知道他们是外向型的。事实上,数学家有各种形状、大小、颜色和外向程度,但是向下看可能会在数学上有所收获。在一次去德国拜访一些数学家朋友的旅行中,我盯着地面看,结果绊倒了——几乎真的被一块美丽的瓷砖图案绊倒了。以下是我盯着它看时的一些粗略的想法记录。
多么漂亮的瓷砖!我想我以前从未见过这样的瓷砖。或者即使见过,我也没注意到。 这些形状有多少条边?1、2、3、4,然后它们都是成对的。八条。这是一个八边形瓷砖。

用白色轮廓勾勒出一个八边形的瓷砖。图片来源:伊芙琳·兰姆
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
非凸形状看起来与凸形状如此不同,这难道不有趣吗?你不能用正八边形平铺欧几里得平面。我想即使这些形状各有八条边,但它们实际上只是伪装成平行四边形或矩形。这种瓷砖的底层图案只是一个网格。

我在一些八边形的中心点上打点,然后用绿色连接它们,以突出显示瓷砖的底层平行四边形网格。 图片来源:伊芙琳·兰姆
这些八边形有四对平行边。这意味着它们是平移曲面! 我敢打赌我的配偶会喜欢这个。他真的很喜欢平移曲面。
在这里,我打断我的意识流回忆,来定义一下平移曲面。它是一个或多个多边形的集合,其中边成对出现,并且平行且长度相同。你可以想象将这些边对粘合在一起,将平面多边形变成一个在空间中弯曲的曲面。环面,或甜甜圈,是一个你可以在家轻松制作的例子。

一个标有边配对的八边形。具有相同标签的边长度相同且平行。图片来源:伊芙琳·兰姆
如果你在一个平移曲面上将相对的边粘合在一起,你会得到某种甜甜圈,也许是带有多孔的甜甜圈。我想知道用这个会得到什么样的甜甜圈。嘿,这附近有甜甜圈店吗?没有?我宁愿要一个椒盐卷饼。
我很难想象如果我将对应的边粘合在一起会发生什么。等等,双正五边形不是有八条边吗?
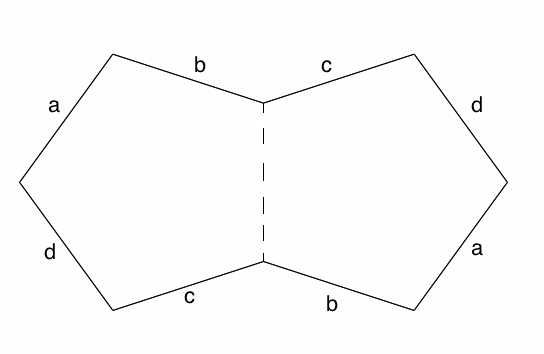
双正五边形的图示,两个五边形沿虚线粘合在一起。标有相同字母的边可以粘合在一起以创建一个曲面。图片来源:伊芙琳·兰姆
戴安娜·戴维斯关于双五边形的“用舞蹈演绎你的博士论文”视频太酷了!我应该再看一遍!
双五边形上的切割序列,通过舞蹈解释,来自 戴安娜·戴维斯,在 Vimeo 上。
铺路石中的八边形与双五边形具有相同的平行边模式,因此它们必定粘合成与双五边形相同类型的曲面。这是一个亏格为 2 的曲面,或是一个有两个孔的甜甜圈。说真的,我现在真的很想吃一些糕点。
等等,如果双五边形是一个八边形,那一定有办法像双五边形那样将铺路石八边形切割成五边形对!
.jpg?w=350)
一张将其中一个八边形切割成两个五边形的图片。图片来源:伊芙琳·兰姆
这意味着这个八边形瓷砖也是伪装成五边形瓷砖!我喜欢五边形瓷砖!我是否发现了一种用五边形平铺平面的新方法?!!

五边形瓷砖用白色勾勒出来。图片来源:伊芙琳·兰姆
这不太可能,对吧?我敢打赌,任何带有直角的五边形瓷砖很久以前就被发现了。我回家后必须查一下。
的确,当我稍后查阅时,我发现这个五边形与下图中的第一种类型的五边形瓷砖相同。这已经为人所知一段时间了。

我该如何平铺你呢?让我数数方法... 图片来源:Ed Pegg Jr. Wikimedia(CC BY-SA 4.0)
五边形中的角是多少度?我没有量角器,但我猜大概是 90-90-130-60-170。
您可能会注意到,铺路石八边形的角度与图表左上角的八边形角度不完全相同。好眼力!已知有 15 种类型的五边形可以平铺欧几里得平面,但其中一些类型具有一些自由度,整个五边形族都可以平铺平面,因为它们满足相同的基本规则。第一种类型的五边形瓷砖包括任何两个相邻角之和为 180° 的五边形。
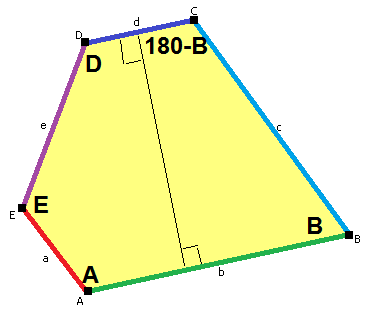
任何满足上述温和条件的五边形,即具有两个相邻角之和为 180° 的五边形,都可以平铺平面。图片来源:Tomruen Wikimedia(CC BY-SA 4.0)
盯着这个瓷砖帮助我理解了为什么这种五边形可以平铺平面。有些点是三个非直角汇聚在一起,有些点是直角与形状的一条边汇聚在一起。任何具有这种性质的五边形都必须可以平铺平面!
所以这是一个八边形瓷砖,它也是一个五边形瓷砖,它建立在底层的四边形瓷砖网格之上。这有多酷?德国有很多这样的瓷砖吗?我应该搬到德国去。
如果我没有注意到这些不寻常的瓷砖并停下来欣赏一会儿,我就永远不会花时间思考为什么这种特定类型的五边形可以平铺平面,并自己弄清楚,而不是听信别人的话。有时候,盯着你的脚下看并不是一件坏事。
要了解更多#foundmath,请在 Instagram 上关注我。
