2018年9月27日

让数学充满乐趣

“数学家在野”詹姆斯·坦顿分享有趣的数学和斯佩纳引理

本文发表在《大众科学》的前博客网络中，反映了作者的观点，不一定反映《大众科学》的观点

在我们播客“我最喜欢的定理”的这一集中，我的联合主持人凯文·克努森和我很幸运地与詹姆斯·坦顿进行了交谈。坦顿博士曾是大学数学家和高中数学老师，但他目前的职称是美国数学协会的“在野数学家”。您可以在这里或kpknudson.com收听该集，那里还有一份文字记录。

关于支持科学新闻

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻报道：订阅。通过购买订阅，您正在帮助确保有关当今塑造我们世界的发现和想法的有影响力的故事的未来。

正如坦顿博士在该集中所说，他认为自己的角色是为所有数学学习水平的学生创造和促进充满乐趣、丰富多彩的数学体验。目前，他对全球数学周特别兴奋，这是一个在10月10日至17日期间将名为“爆炸点”的活动带入世界各地教室的项目。他说，去年，超过一百万学生在课堂上玩过这个活动；今年，他们的目标是 1000 万。

“我最喜欢的定理”是关于定理的，所以我们当然在播客中谈到了一个定理。坦顿博士选择了斯佩纳引理，它与布劳威尔不动点定理有关，弗朗西斯·苏和霍莉·克里格都在他们的播客节目中谈论过这个定理。布劳威尔不动点定理指出，从一个没有孔的域到它自身的函数必须有一个不动点，即被该函数映射到自身的点。斯佩纳引理有点像是那个连续定理的离散版本。

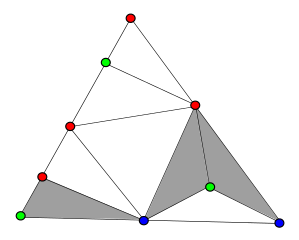
斯佩纳引理的图示，使用颜色而不是字母来标记三角剖分的顶点。斯佩纳引理指出，如果一个端点为红色顶点，另一个端点为蓝色顶点的边有奇数条，那么必须至少有一个三色三角形。来源：Pokipsy76~commonswiki (CC BY-SA 3.0)

坦顿博士解释了如何亲自查看引理。在气球上画一堆点，或者将其展平，然后在纸上的多边形内画一堆点。以某种方式将这些点连接成三角形。现在将每个点标记为 A、B 或 C。无论您如何操作，在气球上，如果您找到一个顶点上都表示三个字母的三角形，那么在某个地方必须还有另一个也具有所有三个字母的三角形。在纸上，您还需要额外的要求，即多边形外部有奇数条“AB”边。（也就是说，连接字母 A 和字母 B 的边。）有几种不同的方法可以陈述引理，所以如果您找到其他版本，您可以尽情找出它们为什么是等价的。

坦顿博士还谈到了如何使用斯佩纳引理来证明毛球定理，这个定理很大程度上因其生动的名称而闻名。这个定理指出，在一个没有孔的毛茸茸的表面上，例如网球或椰子的外部，不可能以平滑的方式梳理毛发，而至少有一根毛发直立着。斯佩纳引理的离散性质，以及其分散的点，与连续的毛球之间的联系让我感到惊讶。

在每集播客中，我们都会要求嘉宾将他们的定理与某事物配对：食物、饮料、艺术、音乐或生活中其他一些乐趣。坦顿博士将斯佩纳引理与他的澳大利亚根源——甜点蛋白饼配对。（对不起我们的新西兰听众；澳大利亚和新西兰都声称拥有蛋白饼，但坦顿博士是澳大利亚人。）您必须收听这一集才能了解为什么这款华丽的蛋白酥皮甜品是斯佩纳引理的完美搭配。

您可以在 Twitter 上和他的网站上找到坦顿博士。有关全球数学周和爆炸点的更多信息，请访问全球数学项目网站和吉姆·普罗普的这篇文章。您可以在 kpknudson.com 和这里的统一的根源找到有关此播客中出现的数学家和定理的更多信息，以及其他有趣的数学内容。文字记录可在此处获得。您可以在 iTunes 和其他播客分发系统上订阅并评论该播客。我们很乐意听取听众的意见，所以请发送电子邮件至 myfavoritetheorem@gmail.com。凯文·克努森在 Twitter 上的账号是 @niveknosdunk，我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 帐户：@myfavethm 和一个 Facebook 页面。下次加入我们，学习另一块引人入胜的数学知识。

此前在“我最喜欢的定理”中