本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在“我最喜欢的定理”这一集中,我的共同主持人凯文·克努森和我很高兴与詹姆斯·麦迪逊大学的数学教授劳拉·塔尔曼交谈。您可以在这里或kpknudson.com收听这一集。
塔尔曼博士多年来戴过许多数学家的帽子,她研究的领域之一是纽结理论。纽结理论学家研究数学纽结,这几乎与您的鞋带或手机充电器线上的纽结相同。您只需将鞋带或线的末端粘在一起,即可得到数学家研究的那种纽结。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保关于塑造我们当今世界的发现和想法的有影响力的故事的未来。
纽结通常以二维图的形式呈现,其中线束相互交叉,纽结理论中最基本的问题是,纽结的两个图何时实际上是同一个纽结。
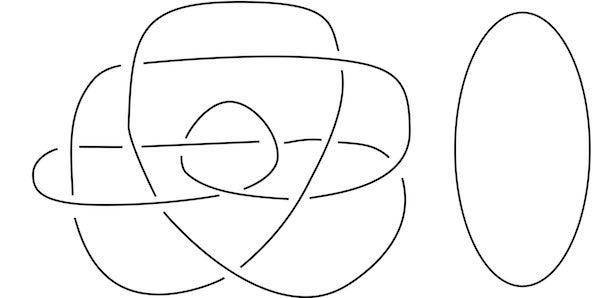
同一个纽结(解结)的两个图。左图来自Mitsuyuki Ochiai的计算机纽结理论导论。来源:基于C S 和 Pbroks13 Wikimedia (CC BY-SA 3.0)
在20世纪20年代,库尔特·莱德迈斯特和其他人表明,如果两个纽结是相同的,则可以使用有限的莱德迈斯特移动序列将一个图变成另一个图。
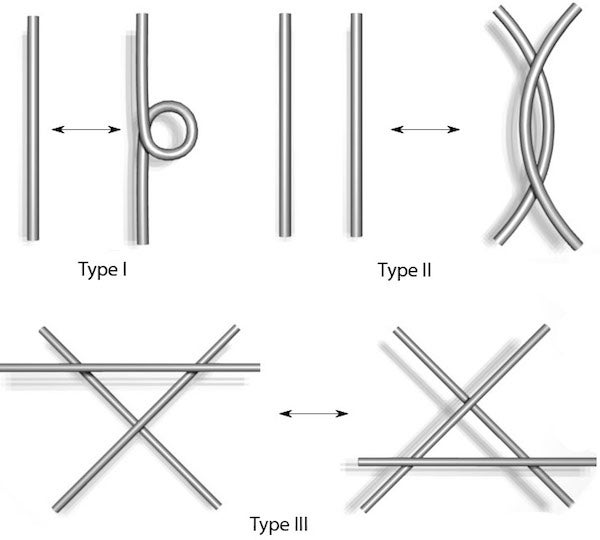
一个图表,说明了三种类型的莱德迈斯特移动。来源:伊芙琳·兰姆,基于Yamashita MakotoWikimedia (CC BY-SA 3.0) 的作品
但是,知道可以使用莱德迈斯特移动将两个等效的纽结图转换为相同的图,其效用是有限的。如果您有两个图并且无法将一个图转换为另一个图,您如何判断这是因为纽结实际上是不同的,而不是因为您只是没有找到正确的移动序列?
塔尔曼最喜欢的定理提供了一种确定纽结是否等效于解结(一个简单的圆圈)的方法。它表明,如果纽结实际上是解结,则根据纽结图中交叉点的数量,将纽结简化为圆圈所需的莱德迈斯特移动次数存在上限。如果您尝试每个可能的移动序列,该序列至少与该上限一样长,并且您的图永远不会变成圆圈,那么您就可以确定该纽结确实是一个纽结,而不是一个解结。(快速说十遍。)
塔尔曼喜欢这个定理,不仅因为它第一次明确给出了这个问题的上限,而且还因为它给出的上限非常夸张。在证明该定理的原始论文中,乔尔·哈斯和杰弗里·拉加里亚斯得到的上限为2n1011,其中n是图中交叉点的数量。那是2的n 百亿次方。哎呀!当您尝试将该数字输入在线计算器Wolfram Alpha时,即使对于非常少的交叉点,计算器也会死机。
塔尔曼博士还向我们介绍了另一篇论文,这篇论文由亚历山大·考沃德和马克·拉肯比撰写,该论文限制了显示任意两个给定纽结图是否等效所需的莱德迈斯特移动次数。该界限涉及幂塔,幂塔的数值也以惊人的速度变得非常大。它们大到我无法描述它们有多大。

为纽结理论和巨大的数字举杯!来源:Maman Voyage Flickr (CC BY-ND 2.0)
在每一集中,我们都会要求嘉宾将他们的定理与某些东西配对。塔尔曼博士选择了一杯美味的香槟来庆祝她最喜欢的定理。您必须收听这一集才能了解她为什么认为这与纽结定理完美匹配。
除了教学和研究工作外,塔尔曼博士还曾在国家数学博物馆担任驻馆数学家一个学期,并在3D打印行业工作过。她现在在课堂上使用3D打印,并在她的博客Hacktastic上发布3D打印教程。她的网站是mathgrrl.com,她的Twitter账号是@mathgrrl。
您可以在kpknudson.com和统一之根找到有关此播客中数学家和定理的更多信息,以及其他令人愉快的数学知识。此处提供文字记录。您可以在iTunes和其他播客分发系统上订阅和评论播客。我们很乐意听到听众的来信,请发送邮件至myfavoritetheorem@gmail.com。凯文·克努森在Twitter上的账号是@niveknosdunk,我的账号是@evelynjlamb。该节目本身也有一个Twitter feed:@myfavethm和一个Facebook页面。请在下次加入我们,了解另一个引人入胜的数学知识。
以前在“我最喜欢的定理”节目中
第 0 集:您主持人的最喜欢的定理 第 1 集:艾米·威尔金森最喜欢的定理 第 2 集:戴夫·里切森最喜欢的定理 第 3 集:埃米尔·戴维·劳伦斯最喜欢的定理 第 4 集:乔丹·埃伦伯格最喜欢的定理 第 5 集:杜萨·麦克达夫最喜欢的定理 第 6 集:惠理子·广中 最喜欢的定理 第 7 集:亨利·福勒最喜欢的定理 第 8 集:贾斯汀·柯里最喜欢的定理 第 9 集:艾米·拉顿斯卡娅最喜欢的定理 第 10 集:穆罕默德·奥马尔最喜欢的定理 第 11 集:珍妮·克莱兰 最喜欢的定理 第 12 集:坎迪斯·普莱斯最喜欢的定理 第 13 集:帕特里克·霍纳最喜欢的定理
