本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点。
.jpg?w=300)
约翰·海因里希·兰伯特。图片来源:公有领域,通过维基共享资源。
双曲几何的历史充满了双曲的引言,我在本学期早些时候的数学史课上偶然发现了一句很精彩的引言。约翰·海因里希·兰伯特是一位1728-1777年间居住的瑞士数学家,他试图证明平行公设,从而毫无疑问地确立欧几里得几何的真理,但最终却证明了一些关于非欧几里得几何的非常奇特的事情。
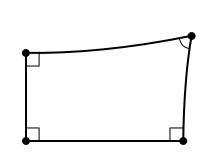
兰伯特对几何学的研究涉及到一个现在被称为兰伯特四边形的图形。(这个名字有些不恰当,因为10-11世纪的阿拉伯数学家伊本·海赛姆在兰伯特之前700多年就使用了它们。)兰伯特四边形有四条边和三个直角。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
在高中几何中,四边形的角之和必须为 360°,但这个事实是基于假设欧几里得平行公设。在欧几里得兰伯特四边形中,第四个角也必须是 90°。兰伯特想要证明第四个角必须是 90°,而无需使用平行公设。为了做到这一点,他探索了与第四个角的角度测量相对应的三种可能性:直角假设、钝角假设和锐角假设。今天,我们会说这三个假设分别对应于欧几里得几何、椭圆或球面几何以及双曲几何。兰伯特发现,在第三个假设下,会发生一些令人困惑的事情:三角形的面积取决于其角之和,并且存在长度的“绝对”度量,也就是说,三角形不能在不扭曲其角的情况下变得更大。这些结果困扰了兰伯特,他写道*
“很容易看出,在第三个假设下,人们可以更进一步,并且在第二个假设下也可以找到类似的但截然相反的结果。但是,在很大程度上,我主要在第三个假设下寻找这样的结果,以便看看是否会出现矛盾。从这一切可以清楚地看出,反驳这个假设绝非易事。我将引用更多结果,而不考虑它们在第二个假设下可以在多大程度上进行扩展,在必要时进行修改。”
“这些结果中最引人注目的是,在第三个假设下,我们将拥有每条线的长度、每个面的面积以及每个物理空间的体积的绝对度量。这驳斥了一些不明智的人认为几何学公理的断言,因为到目前为止,没有人怀疑根本不存在绝对度量。这个结果有些精妙之处,让人希望第三个假设是真的!”
“尽管有这样的收获,但我并不希望如此,因为这会导致无数的不便。三角函数表将无限大,图形的相似性和比例性将完全消失,任何图形都只能在其绝对大小中想象,天文学家将面临困境,等等。”
“但所有这些都是由爱与恨决定的论据,它们在几何学或整个科学中都不应该占有一席之地。”
令人钦佩的是,兰伯特认识到他对第三个假设的含义的反感并没有使其无效。但有趣的是,兰伯特发现绝对长度度量的想法如此令人反感——它就在我们眼皮底下。在球面上,对于任何给定的角集,只有一个大小的三角形。如果你想制作一个更大但具有相同角度的三角形,你必须在更大的球面上绘制它。一旦你确定了一个球体的大小,你就确定了所有三角形的大小。
今天,由于伯恩哈德·黎曼和许多其他人的努力,我们对几何学的概念与兰伯特的概念截然不同。兰伯特试图证明欧几里得几何是*唯一*真正的几何。现在,我们有一种公理化的观点:欧几里得几何是源于欧几里得公理的真正几何,但是如果我们改变这些公理,我们就会得到在不同上下文中有效的不同结果。球面几何从一组不同的公理开始。现代数学家并不认为球面几何是对的,而欧几里得几何是错的,反之亦然。它们只是不同的公理系统。当兰伯特将第三个假设与第二个假设进行比较时,他非常接近这种观点,但他并没有完全达到。他写道
“回到第三个假设[锐角假设]。正如我们刚才所看到的,在这个假设下,每个三角形的三个角之和都小于 180 度,即两个直角。但是,与 180 度的差值像三角形的面积一样增加;这可以这样表示:如果两个三角形中的一个三角形的面积大于另一个三角形,那么第一个三角形的角之和小于第二个三角形……。”
“我只想补充以下评论。完全类似的定理在第二个假设[钝角假设]下成立,只是在第二个假设下,每个三角形的角之和都大于 180 度。超出的量始终与三角形的面积成正比。”
“我认为值得注意的是,如果我们将球面三角形而不是平面三角形,则第二个假设成立,因为它的角之和大于 180 度,并且超出的量也与三角形的面积成正比。”
“更令我震惊的是,我在这里所说的关于球面三角形的内容可以独立于平行线造成的困难来证明,并且仅仅假设每个穿过球体中心的平面都将其分成两个相等部分的公理。”
“由此我几乎可以得出结论,第三个假设在某种虚构的球面上成立。至少一定有什么东西可以解释这样一个事实,即与第二个假设不同,它长期以来一直能够抵制在平面上的反驳。”
虽然双曲几何不在“虚构的球面”上成立(假设他指的是半径为虚数的球面),但兰伯特的观察非常敏锐。球面三角形的面积公式为 K2(a+b+c-180),其中 a、b 和 c 是三角形三个角的度量,K 是一个取决于球面半径的常数。双曲几何中三角形的面积公式为 K2(180-a-b-c)。如果我们想象(哈!)第一个公式中的 K 是一个虚数,那么它的平方是负数,我们就得到了第二个公式。(对于好奇的人来说,在这两种情况下,K 都是包含三角形的曲面的曲率。曲率是我们现代几何处理中的关键构建块之一。)
兰伯特差点取得突破,这将带来几何学的新时代,但这项荣誉最终归于兰伯特去世 50 多年后的亚诺什·波利亚伊和尼古拉·罗巴切夫斯基。尽管如此,他关于爱、恨和虚构球面的话语表明了热情和创造力(以冷静的逻辑为调和剂),这些热情和创造力一直是数学中必不可少的,并最终导致了非欧几里得革命。
* 兰伯特的所有摘录均来自 B.A. 罗森菲尔德的《非欧几里得几何史》的英文翻译。粗体强调是我的。