本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点

一个可穿戴的、针织的 (5,3) 环面纽结。图片来源:sarah-marie belcastro。
让开,无限围巾,你们根本不是无限的。(5,3) 环面纽结颈圈才是潮流。
对我来说,一月份联合数学会议的亮点之一是数学纤维艺术环节。您可以在此处查看我从该环节整理的幻灯片。在会议期间,联合组织者莎拉-玛丽·贝尔卡斯特罗作了关于她美丽的针织环面纽结和链环的演讲。我在幻灯片中加入了一张它们照片,但想在这里的博客上分享更多关于它们的细节。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够持续报道关于发现和塑造我们当今世界的想法的具有影响力的故事。
在数学中,纽结基本上就是现实世界中的纽结。你取一段绳子,以某种方式打结,然后将自由端连接在一起,使其没有起点或终点。(我在去年的博客文章中写过关于纽结的文章,如果您想更深入地了解它们。)链环是任意数量的纽结放在一起。它们可能只是彼此相邻,或者它们可能以某种有趣的方式缠绕在一起。

一个有三个组件的链环。这种配置称为博罗梅安环,它很有趣,因为图片中没有两个圆圈彼此链接,但是当所有三个放在一起时,你无法将它们拉开。图片来源:公共领域,通过维基共享资源。
环面纽结和链环,贝尔卡斯特罗演讲的主题,可以通过将绳子缠绕在环面或甜甜圈上制成。您可以将环面视为当您沿着另一个圆扫过一个圆时获得的形状,如下图所示。
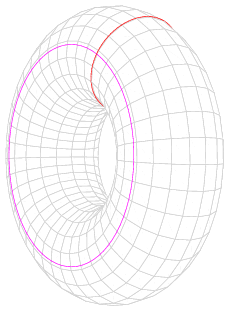
当您沿着粉红色圆圈拖动红色圆圈时,您会得到一个环面。图片来源:Fropuff,通过维基共享资源。
我们可以将红色圆圈和粉红色圆圈,即穿过孔或围绕孔缠绕的圆圈,分别视为环面上的两个主要“方向”,类似于球体上的纬度和经度。
环面纽结或链环由它在两个主要方向上缠绕多少次来定义。一个 (p,q) 环面链环* 穿过中心(沿着红色圆圈)缠绕 p 次,围绕孔(沿着粉红色圆圈)缠绕 q 次。如果我们对 p 或 q 使用负数而不是正数,则描述是相同的,但纽结或链环在环面上以不同的方向螺旋缠绕。有关环面纽结的更多图示,请查看纽结图谱。

一个以 3D 渲染的 (-7,3) 环面纽结。它围绕环面的孔缠绕 3 次,穿过孔缠绕 7 次,但与 (7,3) 环面纽结的扭转方向不同。图片来源:Michiel Sikma,通过维基共享资源。
任何两个整数 p 和 q 都可以定义一个环面链环。如果这些数字没有公因数,则链环只有一个部分,因此我们称之为纽结。如果它们确实有公因数,则链环有多个部分,例如这个 (4,2) 环面链环。(部分的数量与 p 和 q 共享的最大公因数相同。)
-Torus_Link.png?w=500)
一个 (4,2) 环面链环有两个组件。图片来源:公共领域,通过维基共享资源。
贝尔卡斯特罗既是数学家又是编织者,她已经擅长结合这两个学科。她使用数学来理解和指导她的编织,并使用编织来可视化复杂的数学对象。几年前,贝尔卡斯特罗开始编织环面,使用对比鲜明的纱线在上面展示环面纽结。

浅绿色的 (5,3) 环面纽结,背景是深绿色的环面。图片来源:sarah-marie belcastro。
当她继续使用编织来探索数学时,她考虑过去掉环面,只编织纽结本身。当然,一种方法是编织一个细长的矩形,将其打结,然后将两端缝合在一起。但这太容易了!相反,贝尔卡斯特罗想知道她是否可以进行编织,使纽结本质上是由编织创建的,而不是事后添加的。有一天,她将她的环形编织针(这些基本上是两个端点,中间用一根长而柔韧的线连接)打成一个结,最终得到了一个针织的三叶结。

一个三叶结。图片来源:公共领域,通过维基共享资源。
三叶结是除圆圈外最简单的纽结,它也是一个 (3,2) 环面纽结。在成功编织三叶结后,贝尔卡斯特罗想知道她还可以创建哪些其他环面纽结和链环,并最终发现了一种递归算法,用于正确地缠绕针头以编织一些环面纽结。(具体来说,她的程序适用于 (nk+1, k) 环面纽结和 ((n+2)k-1,k) 环面纽结,适用于任何整数 n 和 k。)

一个针织的 (15,5) 环面链环。图片来源:sarah-marie belcastro。
为了创建具有多个部分的环面链环,贝尔卡斯特罗首先使用她的算法编织链环中的一个纽结,然后将其用作链环的下一个组件的基础,她也使用她的缠绕算法创建该组件。她不断这样做,直到她拥有所需的组件数量。因为她将针头缠绕在之前的组件周围以编织每个后续的纽结,所以成品具有所有内置的纽结性和链环性;无需在事后连接末端。

针织环面链环。从左到右,它们是 (4,2)、(6,4) 和 (8,6) 环面链环。每个链环都有两个组件。图片来源:sarah-marie belcastro。
贝尔卡斯特罗说,在编织完环面链环后,项目看起来一团糟。但她已经学会相信,当她从针头上取下它并小心地将其展平时,她将最终得到一个漂亮、正确执行的环面链环。她通常仅出于其数学特性而制作纽结,但最近她发现,通过一些小的调整,她的 (5,3) 环面纽结可以制作成一个漂亮的颈圈。可穿戴的数学,胜出!
*环面纽结可以先标记任一方向。维基百科采用“围绕孔”先出现的惯例,但贝尔卡斯特罗采用“穿过孔”先出现的惯例。这篇文章的原始版本在不同的地方使用了这两种惯例。我已经更新了这篇文章以保持一致,使用贝尔卡斯特罗使用的惯例。如果您最终浏览到维基百科页面,请记住它的环面纽结是使用相反的惯例标记的。