本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
今天在“我的最爱定理”节目中,我的联合主持人凯文·克努森与纽约州立大学奥尔巴尼分校的数学家贾斯汀·柯里对话。他们在加拿大班夫国际研究站举行的拓扑数据分析会议上进行了现场录制。您可以在这里收听,也可以在kpknudson.com收听。
柯里博士最喜欢的定理是柏拉图立体的分类。这些是由全等正多边形构成的五个凸多面体——四面体、立方体、八面体、十二面体和二十面体。四面体、八面体和二十面体分别由四个、八个和二十个等边三角形构成,立方体由六个正方形构成,十二面体由十二个正五边形构成。事实上,没有其他多面体像它们一样规则,这是一个由来已久但仍然美丽而引人注目的定理。
关于支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您将帮助确保未来能够继续报道关于塑造我们当今世界的发现和思想的具有影响力的故事。
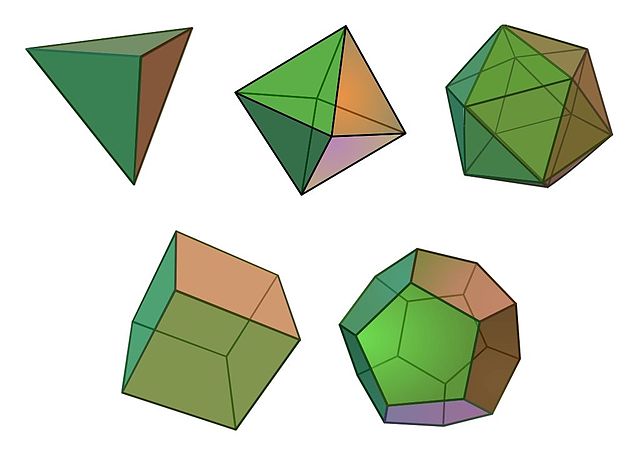
柏拉图立体。顶行:四面体、八面体、二十面体。底行:立方体、十二面体。图片来源: Максим Пе Wikimedia(CC BY-SA 4.0)
他们还谈到了几何学中的对偶性概念。对于任何多面体,你可以用面替换顶点,用顶点替换面,从而得到一个新的多面体。当您对柏拉图立体执行此操作时,您会得到另一个柏拉图立体作为其对偶。立方体是对八面体的对偶,十二面体是对二十面体的对偶,四面体是对自身的对偶。柯里博士非常喜欢这些立体及其对偶性,以至于他纹了关于它们的纹身。他有来自约翰内斯·开普勒的四面体纹身,一个来自艺术家alucinori的立方体-八面体对偶性设计,以及他自己设计的十二面体-二十面体对偶性纹身。如果您还没有准备好达到那种程度的投入,凯文建议您不妨尝试用折纸制作这些立体,可以使用托马斯·赫尔的著作《项目折纸:探索数学的活动》。
在播客的每一集中,我们都会请嘉宾将他们的定理与某事物配对:食物、饮料、音乐、文学或生活中任何其他乐趣。对于他的配对,柯里博士选择了字面意义上的——字面意义上的。他将柏拉图立体与柏拉图的《蒂迈欧篇》配对,柏拉图在其中提出了他对宇宙本质的一些看法。他将四个柏拉图立体——四面体、立方体、八面体和二十面体——与四个元素:火、土、气和水联系起来。十二面体被认为是整个宇宙的形状。您需要收听这一集,才能听到柯里博士关于立体中的对偶性概念如何在这些联系中得到反映的想法。
柏拉图立体对于约翰内斯·开普勒的宇宙学也很重要。他1596年的著作《宇宙神秘论》包含了他的宇宙理论,即宇宙是一组嵌套的柏拉图立体。虽然最终结果并非如此,但它看起来确实很酷。
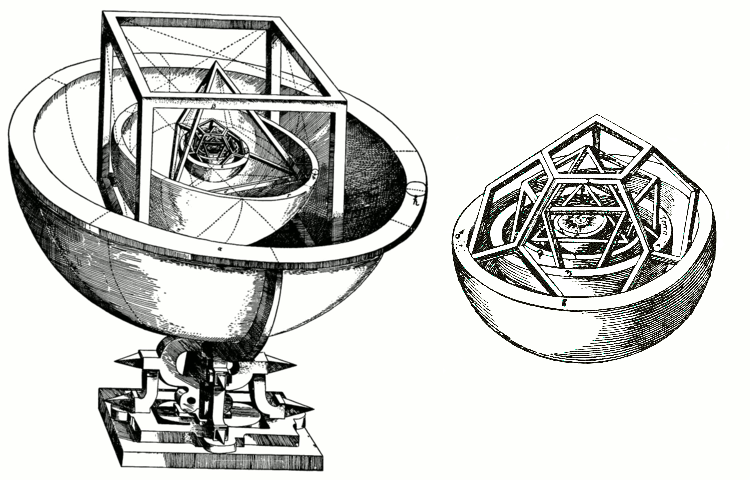
开普勒基于柏拉图立体的太阳系模型,右侧是内行星的细节。图片来源: Mysterium Cosmographicum Wikimedia
您可以在 kpknudson.com 和 “统一的根源”找到更多关于本播客中介绍的数学家和定理的信息,以及其他令人愉悦的数学内容。文本记录在此处提供。您可以在 iTunes 和其他播客分发系统上订阅和评论该播客。我们很乐意听到听众的来信,请发送邮件至 myfavoritetheorem@gmail.com。凯文·克努森的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号: @myfavethm 和一个 Facebook 页面。请在下一次加入我们,学习另一个引人入胜的数学知识。
“我的最爱定理”节目往期回顾
第 0 集:您的主持人们最喜欢的定理 第 1 集:艾米·威尔金森最喜欢的定理 第 2 集:戴夫·里奇森最喜欢的定理 第 3 集:埃米尔·戴维·劳伦斯最喜欢的定理 第 4 集:乔丹·艾伦伯格最喜欢的定理 第 5 集:杜萨·麦克达夫最喜欢的定理 第 6 集:绘里子·广中 最喜欢的定理 第 7 集:亨利·福勒最喜欢的定理
