本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
今天的“我最喜欢的定理”节目邀请了威斯康星大学数学家乔丹·艾伦伯格。您可以在这里收听,也可以访问 kpknudson.com。本集节目中我们遇到了一些音频问题,如果您错过了任何内容,可以访问这里的文字稿。
艾伦伯格最喜欢的定理是费马小定理,这是数论中一个不小的成果。它指出,如果 p 是一个素数(一个正整数,恰好能被两个不同的因子整除:它本身和 1),并且 a 是任何整数,那么 ap 除以 p 的余数为 a。作为简写,数学家会说 ap 与 amod p 同余。(Mod,是 模的缩写,仅表示除以一个数的余数。因此,数字 19 与 4 mod 5 或 1 mod 3 同余,因为它比 15 多 4,而 15 是 5 的倍数,比 18 多 1,而 18 是 3 的倍数。)
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
艾伦伯格陈述了定理在 a=2 特殊情况下的形式。那么定理就变成了当 p 为素数时,2p 与 2 mod p 同余,或者 2p 除以 p 的余数为 2。您可以自己轻松验证一些小的素数 p:23=8,除以 3 的余数为 2。25=32,除以 5 的余数为 2,以此类推。
正如您将在节目中听到的那样,艾伦伯格将费马小定理与帕斯卡三角形的系数联系起来。这个三角形(名称不佳,因为它在帕斯卡接触它之前的几个世纪就已被波斯、印度和中国数学家研究过)以各种不同的形式出现在数学中。要获得帕斯卡三角形中的条目,您从第 0 行中单独的 1 开始。(将此行标记为 0 而不是 1 会使簿记更方便。)然后,每个后续条目都是其对角线上方数字的总和。
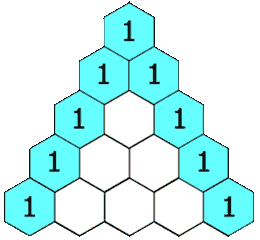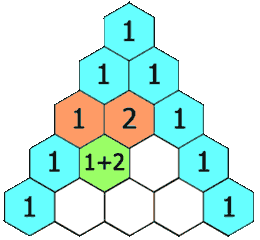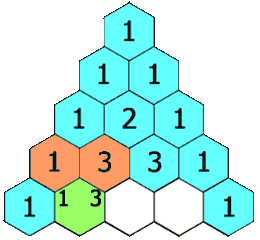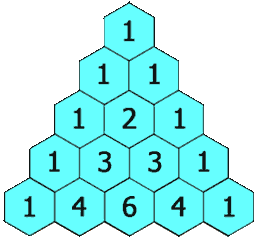
记住我们从第 0 行开始,第 n 行中的数字总和为 2n。

帕斯卡三角形的第 0-9 行。如果您将素数行(如 3 或 7)中的条目相加,然后除以行号,您将始终得到余数 2。
艾伦伯格描述了您如何查看素数行的条目,并几乎可以观察到定理,至少对于 a=2 的情况,就在您眼前显现出来。

盖托斯特奶酪是一种焦糖色的挪威奶酪,与模运算非常搭配。 鸣谢:Maebmij 和 Ranveig Wikimedia(CC BY-SA 3.0)
作为威斯康星州的居民,艾伦伯格感到有义务将他的定理与奶酪搭配。他选择了盖托斯特奶酪,一种焦糖色的挪威奶酪。您需要收听节目才能了解为什么这是费马小定理的完美搭配。
您可以在他的网站 JordanEllenberg.com 和他的 Twitter 帐户 @JSEllenberg 上找到艾伦伯格。他是科普数学书籍 《How Not to Be Wrong》的作者。
您可以在 kpknudson.com 以及这里的 统一性的根源找到有关本播客中数学家和定理的更多信息,以及其他令人愉悦的数学趣味。 文字稿可在此处获取。您可以在 iTunes 和其他播客分发系统上订阅和评论播客。我们很高兴收到听众的来信,所以请给我们发邮件至 myfavoritetheorem@gmail.com。凯文·克努森的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号: @myfavethm 和一个 Facebook 页面。请下次加入我们,学习另一个引人入胜的数学知识。
以前在“我最喜欢的定理”节目中
第 0 集:您的主持人们最喜欢的定理 第 1 集:艾米·威尔金森最喜欢的定理 第 2 集:戴夫·里切森最喜欢的定理 第 3 集:埃米尔·戴维·劳伦斯最喜欢的定理
