本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在今天的“我最喜欢的定理”节目中,我的联合主持人凯文有机会与科罗拉多大学博尔德分校的数学教授 Jeanne Clelland 进行了交谈。他们去年夏天在塔夫茨大学的度量几何和选区划分小组会议上亲自录制了这期节目,我没能参加。您可以在这里或 kpknudson.com 收听这期节目。
Clelland 选择了 高斯-博内定理 作为她最喜欢的定理,我必须说她提出了一个非常有说服力的理由,以至于我正在认真考虑用高斯-博内定理来换取 我的单值化定理。我们一直在我们的 Twitter 和 Facebook 页面上使用高斯-博内定理作为我们的横幅图片,所以 Clelland 博士确保我们没有做任何虚假宣传真是太好了!
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您将帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的具有影响力的故事。
高斯-博内定理真是一个奇迹。就像我最喜欢的定理和 Emille Davie Lawrence 最喜欢的定理 一样,它是关于二维表面的。虽然有一些推广,但 Clelland 博士专注于紧凑的二维表面的情况,这意味着它们是有限且无穿孔的,就像甜甜圈的釉面或椒盐卷饼的表面。
高斯-博内定理指出,这种表面的总曲率,或曲率在表面上的积分,仅取决于它拥有的孔的数量,也称为它的亏格。一个球体的亏格为 0,一个环面或甜甜圈的亏格为 1,以此类推。
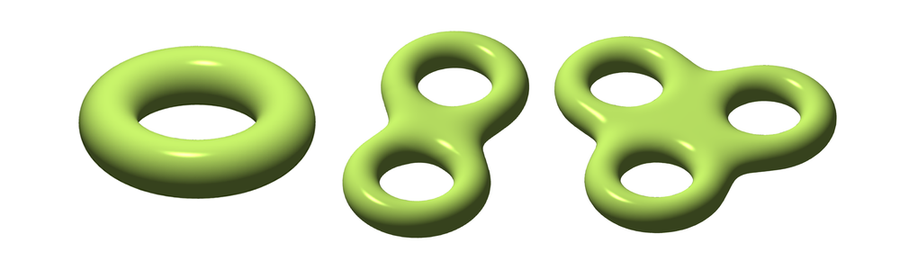
从左到右:亏格为 1、2 和 3 的表面的图片。图片来源:基于 Oleg Alexandrov 的图片
表面的曲率是一种量化表面弯曲程度的方法。如果在给定点,表面上的每条线都从切平面向同一方向弯曲(就像球体上的线一样),那么该点就具有正曲率。如果表面上的一些线在一个方向弯曲,而另一些线在另一个方向弯曲(就像马鞍从前向后向上弯曲,从一侧到另一侧向下弯曲一样),则该表面在该点具有负曲率。如果表面沿着某条线没有弯曲,例如圆柱体的“高度”方向,则它具有零曲率。当表面几乎平坦时,曲率接近于零,而当表面非常弯曲时,曲率远离零。因此,沙滩球在任何给定点的曲率都比弹珠低。

从左到右:具有负曲率、零曲率和正曲率的表面。图片来源:Jhausauer Wikimedia
曲率可以在表面上变化,但高斯-博内定理指出,它总是以某种方式平衡,这种方式仅取决于其亏格。当我进行研究时,我研究的表面具有恒定曲率,因此高斯-博内定理意味着我可以仅根据表面的亏格来确定表面的面积。Clelland 博士还指出了高斯-博内定理与球体上三角形的面积公式之间的关系。
Clelland 决定避开明显的(但美味的)甜甜圈或百吉饼与高斯-博内的搭配,而是建议焰火表演和 柴可夫斯基的《1812序曲》。您可以收听这期节目,了解它们为何与高斯-博内定理如此相配。
Clelland 是 《从弗雷内到嘉当:移动标架法》 一书的作者,这是一本关于微分几何的高级本科或研究生水平的教科书。您可以在 kpknudson.com 和 Roots of Unity 上找到有关此播客中出现的数学家和定理以及其他令人愉悦的数学知识的更多信息。 此处提供文字稿。您可以在 iTunes 和其他播客传送系统上 订阅和评论该播客。我们很乐意听到听众的来信,所以请发送邮件至 myfavoritetheorem@gmail.com 联系我们。Kevin Knudson 的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。请在下次加入我们,学习另一个引人入胜的数学知识。
“我最喜欢的定理”节目回顾
第 0 集:您的主持人们最喜欢的定理 第 1 集:Amie Wilkinson 最喜欢的定理 第 2 集:Dave Richeson 最喜欢的定理 第 3 集:Emille Davie Lawrence 最喜欢的定理 第 4 集:Jordan Ellenberg 最喜欢的定理 第 5 集:Dusa McDuff 最喜欢的定理 第 6 集:Eriko Hironaka 最喜欢的定理 第 7 集:Henry Fowler 最喜欢的定理 第 8 集:Justin Curry 最喜欢的定理 第 9 集:Ami Radunskaya 最喜欢的定理 第 10 集:Mohamed Omar 最喜欢的定理
