本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在我们的播客“我最喜欢的定理”这一集中,我的联合主持人凯文·克努森和我很高兴与来自中国深圳南方科技大学的 Jana Rodriguez Hertz 交谈。您可以在此处或在 kpknudson.com 上收听该节目,其中还有一份文字稿。
罗德里格斯·赫兹博士选择在节目中谈论史蒂芬·斯梅尔的马蹄形映射。但首先她谈到了面条。她拍摄了一段视频,记录了她校园食堂的一位厨师制作面条的过程。厨师拉伸面条,将面条自身折叠起来,然后再拉伸,重复几次步骤,然后将面条扔进锅里。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过 订阅来支持我们屡获殊荣的新闻工作。通过购买订阅,您将有助于确保关于塑造我们当今世界的发现和想法的具有影响力的故事的未来。
这个过程很像马蹄形映射。马蹄形映射是从一个正方形到它自身的一个函数。首先,您通过在一个方向上挤压并在另一个方向上拉伸来使正方形变形,这样您就得到一个长而窄的条带,其面积与原始正方形相同。现在,您将条带折叠成马蹄形,使其 1/3 位于正方形的 1/3 中,1/3 位于另一个正方形的 1/3 中,中间的 1/3 形成马蹄形的弯曲部分。出于此映射的目的,我们将丢弃中间的 1/3,即没有回到原始正方形的部分。在下图所示,正方形的左 1/3 已映射到正方形的底部 1/3,正方形的右 1/3 已映射到正方形的顶部 1/3。(在播客节目中,罗德里格斯·赫兹博士描述了该图中地图的旋转版本。这个想法是一样的。)
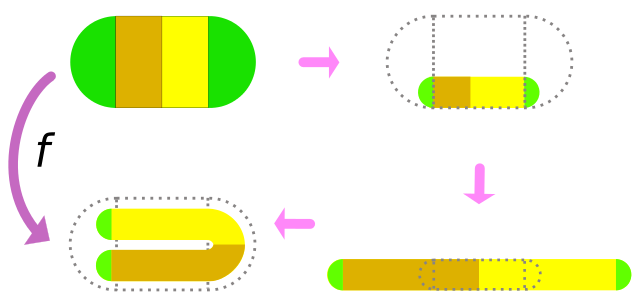
斯梅尔马蹄形映射的示意图。图片来源:SyntaxError55 Wikimedia(CC BY-SA 3.0)
如果您只执行一次映射,那么它并没有那么令人印象深刻,但如果您像厨师做面条那样执行一次变换,然后再执行一次又一次,您就会开始得到一些很酷的东西,而这种酷行为是罗德里格斯·赫兹博士最喜欢的定理。大多数点最终都会被丢弃,因为它们在某个时间被卡在马蹄形的弯曲部分中,但留在正方形中的部分会被拉伸成康托集的面条状版本。(在此处阅读有关康托集的更多信息。)

创建康托集的无限过程的七次迭代。图片来源:127rect Wikimedia
您还可以想象反向运行映射。不是正方形的顶部 1/3 映射到左 1/3,底部映射到右 1/3,而是得到正方形的左 1/3 映射到顶部 1/3,右 1/3 映射到底部 1/3。您可以问,无论向前还是向后,是否会有任何点永远留在正方形中,而且确实有一些。永远停留的点,也称为不变集,形成一个名为康托尘埃的空间。

康托尘埃是两个康托集的乘积,就像平面是两条直线的乘积一样。图片来源:Solkoll Wikimedia
正如罗德里格斯·赫兹博士所描述的那样,马蹄形映射生动地说明了从一个相当简单的系统中产生的混沌行为。混沌的标志之一是混沌系统对初始条件非常敏感,马蹄形映射也适用。无论两个点彼此有多近,最终它们的行为都将完全不同。事实上,正如她所提到的,您实际上可以通过记录它在此映射的迭代下所去的位置来完全且唯一地描述一个点,这个想法与所谓的符号动力学相关。罗德里格斯·赫兹博士还提到了一个名为帐篷映射的映射,这是另一个具有混沌行为的简单系统。您可以在此处阅读更多相关信息。
她还提到了马蹄形映射与一个名为符号动力学的领域的联系。符号动力学的基本思想是,您可以使用有限数量的字母或数字来编码系统中经历变换的点的行为。在马蹄形映射的情况下,她描述了如何用 0 和 1 的序列来描述不变集中的每个点,它们代表了它在每个步骤中(向前和向后)所处集合的哪个部分。
.JPG?w=450)
罗德里格斯·赫兹博士与斯梅尔马蹄形映射的同名者史蒂芬·斯梅尔合影。图片来源:Jana Rodriguez Hertz
在播客的每一集中,我们都会请嘉宾将他们的定理与某个事物配对。罗德里格斯·赫兹博士出生于阿根廷,在搬到中国之前在乌拉圭工作了很多年,她即兴发挥了一个想法,即马蹄形映射中的一个点完全由它的路径决定,并谈到了这个想法如何在她的生活中产生共鸣。您必须收听这一集才能了解完整的故事。我认为有趣的是,她和艾米·拉敦斯卡娅(她与我们谈论了伯克霍夫遍历定理)都来自动力系统领域,他们都在哲学上探讨了如何将他们的定理视为隐喻。
您可以在 Twitter 上关注罗德里格斯·赫兹博士。您可以在kpknudson.com和“统一之根”中找到有关此播客中出现的数学家和定理的更多信息以及其他令人愉悦的数学信息。 此处提供文字稿。您可以在 iTunes 和其他播客传输系统中订阅和评论该播客。我们很乐意收到听众的来信,因此请通过myfavoritetheorem@gmail.com给我们留言。凯文·克努森在 Twitter 上的账号是@niveknosdunk,而我的账号是@evelynjlamb。该节目本身也有一个 Twitter 动态:@myfavethm和一个Facebook 页面。下次加入我们,学习另一件引人入胜的数学知识。
“我最喜欢的定理”之前的内容
第 0 集:您主持人的最爱定理 第 1 集:Amie Wilkinson 最喜欢的定理 第 2 集:Dave Richeson 最喜欢的定理 第 3 集:Emille Davie Lawrence 最喜欢的定理 第 4 集:Jordan Ellenberg 最喜欢的定理 第 5 集:Dusa McDuff 最喜欢的定理 第 6 集:Eriko Hironaka 最喜欢的定理 第 7 集:Henry Fowler 最喜欢的定理 第 8 集:Justin Curry 最喜欢的定理 第 9 集:Ami Radunskaya 最喜欢的定理 第 10 集:Mohamed Omar 最喜欢的定理 第 11 集:Jeanne Clelland 最喜欢的定理 第 12 集:Candice Price 最喜欢的定理 第 13 集:Patrick Honner 最喜欢的定理 第 14 集:Laura Taalman 最喜欢的定理 第 15 集:Federico Ardila 最喜欢的定理 第 16 集:Jayadev Athreya 最喜欢的定理 第 17 集:Nalini Joshi 最喜欢的定理 第 18 集:John Urschel 最喜欢的定理 第 19 集:Emily Riehl 最喜欢的定理 第 20 集:Francis Su 最喜欢的定理