本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定代表《大众科学》的观点。
佛罗里达大学数学家Kevin Knudson和我很高兴地宣布我们的新数学播客:我最喜欢的定理。在每一集中,理所当然地,我们都会邀请一位数学家来讲述他们最喜欢的定理。因为生活中美好的事物在一起会更好,我们还会请嘉宾将他们的定理与任何东西搭配:葡萄酒、啤酒、咖啡、茶、冰淇淋口味、奶酪、最喜欢的音乐作品,等等。我们希望您会喜欢学习一些优美数学定理的完美搭配。
我们对这个播客感到非常兴奋,并希望您能在网站页面上或任何您获取播客的地方收听。新剧集大约每三周发布一次。到目前为止,我们已经有了一系列优秀的嘉宾阵容,我们认为您会喜欢听到来自不同数学领域、地理位置和数学职业的数学家的声音。
我们决定从一集只介绍我们两个人和我们最喜欢的定理开始。您可以在这里或kpknudson.com上收听,该网站还提供了该集的文字稿。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您将有助于确保未来继续有关于塑造我们当今世界的发现和思想的具有影响力的报道。
那么我们最喜欢的定理是什么呢?我们不久前,在 3 月 23 日,艾米·诺特生日那天录制了这一集。我差点选择了诺特定理,这是物理学中的一个重要定理。它将物理系统的对称性与守恒定律联系起来,正如这段视频所解释的那样。
但我没有选择诺特定理。它不是我真正最喜欢的,我只是太诚实了。相反,我选择了单值化定理。这是拓扑学中的一个定理,它指出二维表面可以有三种基本几何形状:球面几何(也称为椭圆几何)、欧几里得几何(也称为平面几何)和双曲几何。球面几何,顾名思义,就是你生活在球体表面所得到的几何形状。“直线”是大圆,就像我们的赤道或经线一样,它们都相交。欧几里得几何,或平面几何,是经典的二维平面。欧几里得平面中的平行线永远保持相同的距离。双曲几何是你在羽衣甘蓝上的蚜虫或珊瑚礁上的微小海洋生物所居住的那种仙境。在那里,平行线彼此远离。
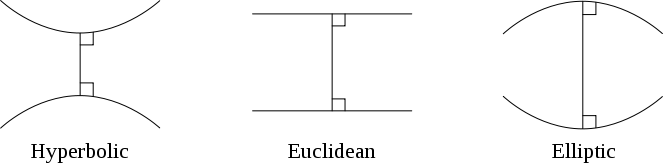
双曲几何、欧几里得几何和椭圆几何(或球面几何)的示意图。在双曲几何中,平行线彼此远离。在欧几里得几何中,它们保持相同的距离,而在椭圆几何中,没有不相交的线。图片来源:Pbroks13 和 Joshuabowman Wikimedia(CC BY-SA 3.0)
从技术上讲,单值化定理只适用于没有孔的表面(用更专业的术语来说,是单连通的),但该定理可以用来证明有孔的表面——甜甜圈、椒盐卷饼和其他有许多孔的形状——也可以分为这三种类型的几何形状。(我们使用术语亏格来描述表面拥有的孔的数量。)

冰爽夏日美食还是单值化定理的可食用插图?为什么不两者兼得?图片来源:Pschemp WIkimedia(CC BY-SA 3.0)
我选择了那不勒斯冰淇淋作为单值化定理的完美搭配。二维几何有三种口味:球面、欧几里得/平面和双曲。那不勒斯冰淇淋是将巧克力、香草和草莓混合在同一个美味纸盒中的冰淇淋。您需要收听该集才能找出哪种几何形状与哪种口味搭配。

我最喜欢的定理联合主持人 Kevin Knudson。图片来源:Kevin Knudson
Knudson 选择了火腿三明治定理。如果您有两片面包和一块火腿,您可以(如果您找到一把能够胜任的刀)仅用一刀将所有三个质量精确地切成两半。对于传统构造的三明治来说,这似乎是合理的,但即使您非常马虎地将火腿放在面包上,或者甚至将面包放在盘子上并将火腿放在冰箱中,这也是正确的。总有一个切割平面可以将所有质量平分。如果您想平分一个更复杂的三明治,您可以……只要您用更高维度的材料制作三明治即可。您想要平分的质量数量决定了您的三明治必须存在的维度。
.JPG?w=300)
享用火腿三明治定理的完美啤酒。图片来源:Kevin Knudson
三明治并不花哨,所以 Knudson 选择用啤酒搭配他的定理。具体来说,他认为来自盖恩斯维尔 First Magnitude Brewing 的72 Pale Ale是完美搭配。
您可以在kpknudson.com和《单位根》这里找到更多关于本播客中介绍的数学家和定理的信息,以及其他令人愉悦的数学知识。文字稿可在此处获取。您可以在 iTunes 或任何您获取播客的地方订阅和评论播客。我们很乐意听取听众的意见,请发送邮件至 myfavoritetheorem@gmail.com 与我们联系。Kevin Knudson 的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。下次加入我们,学习另一个引人入胜的数学知识。