本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定反映《大众科学》的观点
前几天,我在我最喜欢的博客之一数学教授语录上看到一句话,有点让我震惊:“宇宙中任何数的 log log 值实际上都小于 5。”
如果您的高中数学知识有点模糊,那么数的对数(logarithm 的缩写)基本上就是它的数量级。目前尚不清楚这位匿名数学教授说的是以 10 为底的对数还是自然对数,还是他或她偏爱的其他对数,但这其实并不重要。 想法是一样的。
更技术性地说,如果 y=log(x),并且我们讨论的是以 10 为底的对数,这意味着 y 是使 10y 等于 x 的数。所以 log(10)=1,log(100)=2,因为 10^1=10,10^2=100。* 对数是指数函数的反函数。 我认为它是一种“扁平化”函数:介于 10 和 100 之间的所有数的对数都在 1 和 2 之间,介于 100 和 1000 之间的所有数的对数都在 2 和 3 之间。 差异被扁平化了。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的具有影响力的故事的未来。
那么,一个数的 log log 值是数量级的数量级。 它使数字更加扁平化。 正如指数增长速度快于乘法(并且 向上箭头 增长速度快于指数),log 增长速度慢于乘法,log log 增长速度慢于 log。 虽然 log 10 和 log 100 相差 1,但它们的 log log 值仅相差 0.3。 直到 10,000,000,000,log log 值才达到 1。
那么,宇宙中任何数的 log log 值都小于 5 吗? 现在,教授所说的底数可能很重要。 如果教授指的是以 10 为底的对数,那么任何小于 10105 的数(即 1 后面跟 100,000 个零)的 log log 值都小于 5。 我不知道您怎么样,但在我的日常生活中,我并不经常需要这么大的数字。
但是,我猜这位好教授可能指的是自然对数,或者 以 e 为底的对数,因为那是数学家通常使用的对数。 我将把它写成“ln”以避免歧义,尽管我会注意到,在我的脑海里,我仍然把它发音为“log”。
即使是以 e 为底数,ln ln 值为 5 的数也大得难以置信。 数 ee5 大约是 3x1064,因此任何小于该数的数的 ln ln 值都小于 5。 我很少甚至只是转瞬即逝地想到这么大的数字。 作为参考,宇宙中大约有 1080 个原子。 如果我们经常谈论所有原子,我们就需要一个 ln ln 值为 5.2 的数。 向上舍入到 googol 也不会改变太多:现在我们大约是 5.4。
思考 log log 的增长速度有多慢以及它使数轴扁平化的程度,我开始思考我在微积分第二学期第一次遇到的一些无穷级数,它们仍然让我着迷。 首先,是调和级数
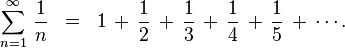
调和级数是发散的,这意味着即使项变得越来越小,总和也是无穷大的。(我不会剥夺您弄清楚它为什么是无穷大的乐趣,但我会给您一个提示:考虑对项进行分组,看看您是否可以将所有组都变得大于 1/2。)
尽管调和级数是发散的,但它的发散速度非常慢。 本·奥林报告说,googol 项之后的总和约为 230。 换句话说,通过微小的分数向上计数是达到无穷大的一种低效方法。
这与 log log 有什么关系呢? 嗯,有一个发散级数,它比调和级数更慢地逃逸到无穷大:从 2 到无穷大的 1/n(ln(n)) 的和。(为什么要从 2 到无穷大而不是从 1 开始? 如果我们试图包含 n=1 项,我们就会被除以 ln(1)(也称为 0)所造成的灾难所吞噬。)
让我们思考一下级数 ∑1/n(ln(n)) 正在发生什么。 每一项都小于调和级数的对应项,调和级数是发散的。 另一方面,它大于 1/n2 的对应项,而 1/n2 是收敛的。
幸运的是,我们可以引入一些积分来使我们自己确信 ∑1/n(ln(n)) 确实是发散的。 函数 1/x 有点像序列 1/n。 该函数只是在序列的步骤之间进行插值。

函数 y=1/x 的图以及高度均为 1/n 的步骤(对于 n=1、2、3 等)。 函数 1/x 曲线下的面积被深色阴影覆盖,步骤下的面积被浅色阴影覆盖。 图像使用 Desmos 创建。
函数 y=1/x 的积分(上面曲线下的面积)与级数 ∑1/n 的和相关:要么两者都是有限的,要么两者都是无限的。 这为我们提供了一种不太有趣的方法来证明调和级数是发散的:1/x 的积分是 ln(x),它会任意增长,因此从 x=1 一直到无穷大的曲线下面积是无限的。
一般来说,将无穷级数与连续函数的积分进行比较是了解和是否有限或无限的好方法。 对于级数 ∑1/n(ln(n)),我们将它与函数 y=1/x(ln(x)) 进行比较。 如果我们可以弄清楚 1/x(ln(x)) 的积分是否有限,我们就会知道该级数是否收敛。
这里的细节并不重要,但事实证明 1/x(ln(x)) 的积分是 ln(ln(x)),我们心爱的 log log。 再次,一个数的 log log 值可以达到的值没有界限,因此从 2 到无穷大的 1/x(ln(x)) 的积分和从 2 到无穷大的 1/n(ln(n)) 的和都是无限的。
如果您认为调和级数发散得很慢,那么您会被 ∑1/n(ln(n)) 震惊到。 在 googol 项之后,调和级数的和为 230。 1/n(ln(n)) 的前 googol 项的和约为 ln(ln(one googol)),您可能还记得它是 5.4。 如果您想通过步长为 1/n(ln(n)) 的步子一直走到 230,您将需要走很长一段时间。
但是等等,还有更多!(或者更少,取决于您如何看待它。) 宏伟的链式法则 使我们能够构建一整套都趋于无穷大的级数,每个级数都比上一个级数更慢。 我们只需开始堆叠对数即可。

它很快就变得很荒谬。 ∑1/n(ln(n))(ln(ln(n))) 的和有点像 1/x(ln(x))(ln(ln(x))) 的积分。 该积分是 ln(ln(ln(x))),因此 ∑1/n(ln(n))(ln(ln(n))) 一直到 googol 的和约为 1.69。
级数 ∑1/n(ln(n))(ln(ln(n)))(ln(ln(ln(n)))) 的增长速度甚至更慢。 我们与之比较的函数 1/x(ln(x))(ln(ln(x)))(ln(ln(ln(x)))) 的积分是 ln(ln(ln(ln(x))))。 在 googol 处,该值略高于一半。
我们可以整天不断添加对数,并获得发散速度越来越慢的级数。 我正在掩盖的一个奇怪之处是找到每个级数或积分的正确起点。 您不想意外地除以 0 或尝试取负数的自然对数,因此您必须比上一个级数稍晚开始每个级数,以避免这些复杂情况。
我想不出任何实际理由让我想要找到从 n=16 开始的 ∑1/n(ln(n))(ln(ln(n)))(ln(ln(ln(n)))),但我认为思考这些痛苦地缓慢的通往无穷大及更远的路程很有趣。 毕竟,生活在于旅程,而不在于目的地。
*如果您是在新版本的《大众科学》网站上查看此帖子,则指数的格式可能不正确。 页面顶部可能会有一个选项,可以在旧版本的网站上查看它。
