本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
玛丽安·米尔扎哈尼于7月14日去世。她是一位杰出的数学家,并在2014年成为首位女性和首位伊朗人获得著名的菲尔兹奖时一举成名。她年仅40岁。她本应拥有更美好的未来。 她的去世是数学界的巨大损失。
米尔扎哈尼的讣告, 包括我写的那篇, 倾向于提及她对双曲几何和台球的兴趣。这些文章中不太清楚的是这两个领域是如何联系起来的。简而言之,我们可以通过将台球桌展开成可以支持双曲几何的表面来连接这两个领域。
双曲几何是研究自然几何形状处处呈马鞍状的曲面的学科。局部来看,二维物体,如沙滩球或百吉饼的表面,可以具有三种不同的几何形状之一:正曲率(像球体一样弯曲)、负曲率(像马鞍或品客薯片一样弯曲)或平坦(像一张纸或桌面)。此外,曲面可以根据整个物体的“自然”几何形状类型进行分类。一个放在我们真实三维世界中的百吉饼,有些地方像球状,有些地方像马鞍状,但作为一个抽象的表面,它的“自然”几何形状实际上是平坦的。看到这一点的其中一种方法是,你可以通过将边缘粘合在一起,用一张平纸构建一个类似百吉饼的形状,或环面。有关更多信息,请参阅这篇关于环面的文章。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业: 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。
没有孔洞的物体,如沙滩球,自然是正曲率的(也称为球面几何),而有很多孔洞的物体,如椒盐卷饼,则具有自然的负曲率(也称为双曲几何)。米尔扎哈尼研究了有很多孔洞的曲面。
这些曲面通常来自台球桌。尽管数学家关心各种不同形状的台球桌,但我们不妨从矩形桌子开始,看看我们如何从一个平面矩形(台球在上面弹跳)到一个曲面,在本例中是一个环面。我在一篇关于我最喜欢的空间之一的文章中写到了这一点,沿狭缝粘合的两个环面,所以这个解释是从那篇文章改编而来的。
数学台球是理想化的。没有摩擦会减慢它们的速度。 与具有一定面积的球不同,一个点沿直线运动,直到它撞到桌子的边缘,此时它与边缘发生完全弹性碰撞,并沿另一个方向继续前进。(入射角等于反射角,因此如果它正面撞击台球桌的边缘,它将沿同一方向反射回来。如果它以 30° 角撞击,它将以 30° 角弹开。)
所有这些弹跳和方向改变使得跟踪轨迹变得复杂,因此数学家采用了一个巧妙的技巧来简化他们的问题:他们展开桌子。当球撞到边缘时,我们不是反射球的轨迹,而是反射桌子,球继续不受阻碍地前进。这样,方向永远保持不变。为了了解这在矩形中是如何工作的,我们将跟踪一个点来看看会发生什么。
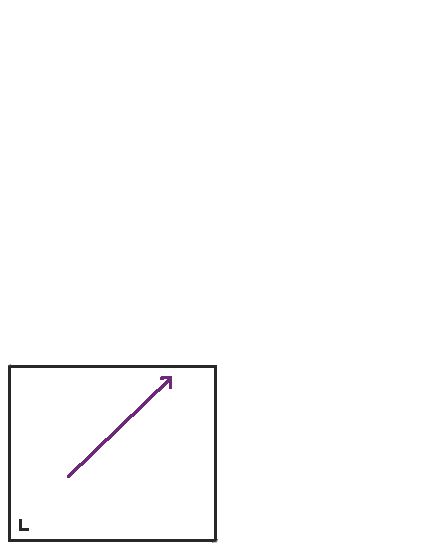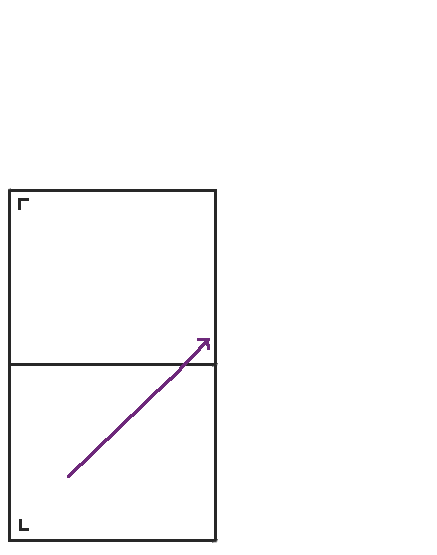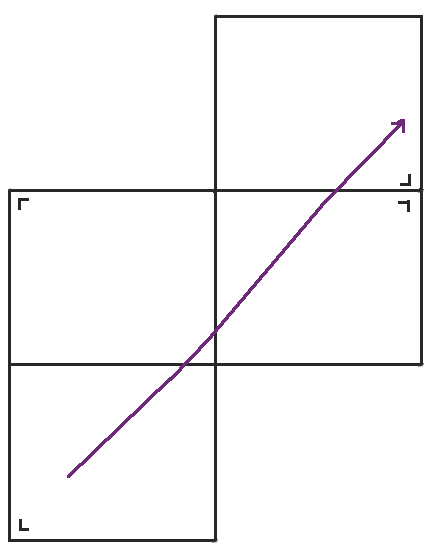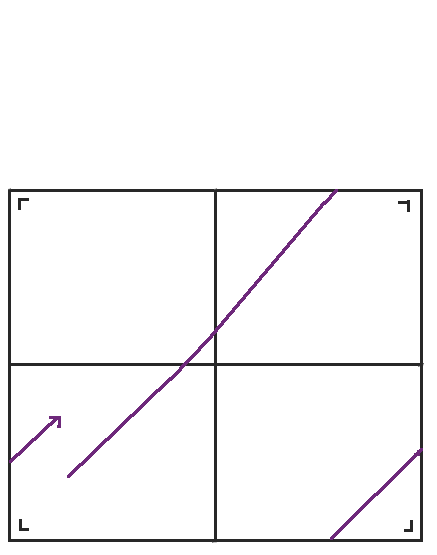
首先,我们从在一个矩形中向东北方向移动开始。我在左下角用一个小 L 标记了矩形,以便我们在展开桌子时跟踪桌子的方向。
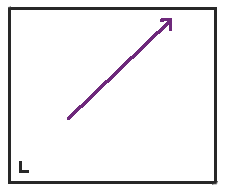
当我们到达矩形的顶部时,我们不是弹回,而是将桌子沿顶部反射,然后点继续前进。
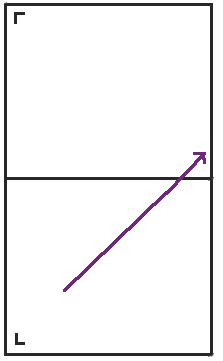
当我们到达桌子的右侧时,我们将桌子沿右侧反射并继续前进。

当我们到达那个桌子的顶部时,我们再次反射。
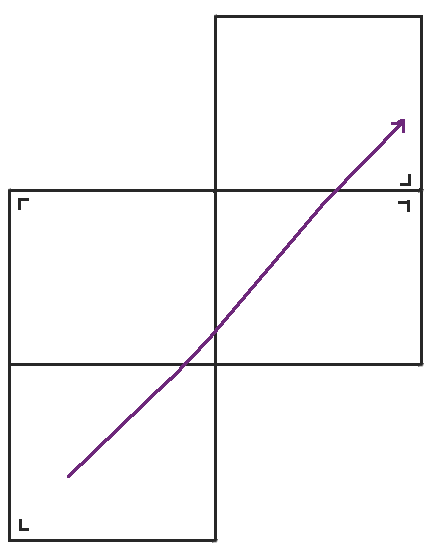
当我们到达右侧时,我们可以再次反射桌子,但是左下角的桌子与我们将得到的桌子具有相同的方向,所以我们不妨再次跳回到左下角的桌子。当我们稍微重新排列桌子时,我们得到了我们熟悉的环面,一个顶部粘到底部,左侧粘到右侧的矩形。

这是整个过程的 gif 动画。
通过这种方式,我们从矩形上的台球运动过渡到环面上的直线流。我在研究生院看过几次这个展开演示,我感觉非常自信我理解了它。但是矩形是一个简单的形状。最后,它展开成一个自然平坦的表面。我是否可以执行这个展开程序并获得一个自然双曲的表面? 在下一篇文章中,我将写下当我尝试展开五边形台球桌时发生的事情。