本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
这一切都始于粗糙的斜裁滚边。斜裁滚边是用沿织物对角线(“斜纹”)裁剪的布条制成的,使其比平行于纹理裁剪的布条更具弹性和延展性。它的柔韧性使其非常适合包边弯曲边缘。不幸的是,我为最近的项目——给新生婴儿制作围兜——购买的斜裁滚边是一种粗糙的涤纶。我没有尝试寻找颜色搭配良好的棉质滚边,而是决定用剩下的布料自己制作。
制作斜裁滚边的一种方法是将几条斜纹布条裁剪下来,缝合在一起,然后将它们穿过您方便的斜裁滚边器。这种方法是最直接的方法,但它也有缺点。您必须一次缝制许多接缝,并且最终会得到一些烦人的小布料碎片,这些碎片真的不值得缝合在一起而被扔掉。

关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
几年前,一位朋友分享了一个制作连续滚边的惊人教程。我使用过这个教程几次,它总是让我感到惊叹。链接中有完整的详细信息,但主要思想是,您不是裁剪对角线布条然后再缝合在一起,而是在裁剪出来之前先将它们缝合在一起。
您从一块正方形的布料开始,然后沿着其中一条对角线裁剪,并将顶部缝合到底部。
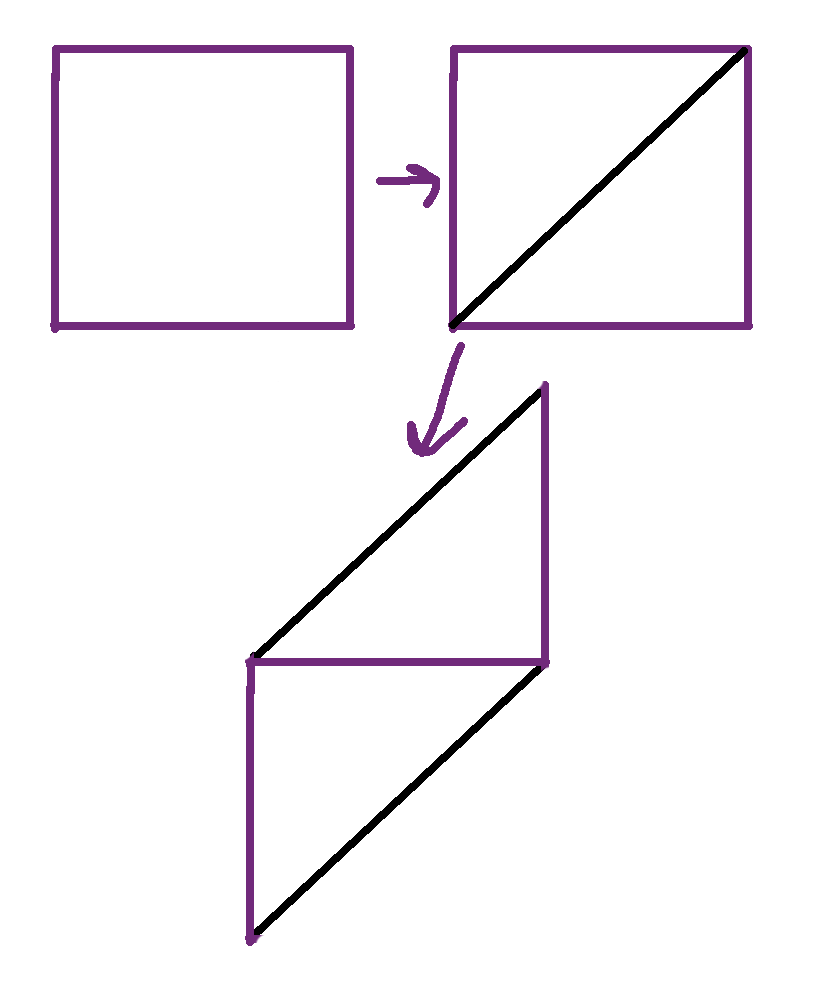
此时,您可以裁剪一堆长度相同的斜纹布条,然后将它们逐个缝合在一起,但该教程仍然更聪明:您将左右两侧缝合在一起。如果您将它们缝合得完美对齐,您最终只会得到一堆布料环。相反,您稍微偏移它,使其在您完成时自然地流动成一条长布料。
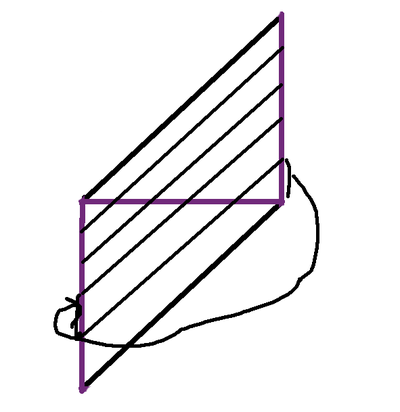
我已经使用过这个教程几次了,它总是让我感到高兴。当您开始裁剪并最终得到您想要的斜纹布条时,这几乎是神奇的。最近一次我制作它时,我专注于这个过程的拓扑结构。当您将顶部缝合到底部并将左侧缝合到右侧时,您正在制作一个奇怪的环面。由于侧面的偏移,它与环面的漂亮矩形图片不太一样,但这给了我一个想法:我可以先制作奇怪的环面,然后沿对角线裁剪以裁剪出布条吗?我必须尝试一下!
首先,我从布料上裁剪出一个正方形,并在上面画出对角线,以帮助我对齐我的工作。

然后我缝制了第一条接缝,将正方形变成一个管状。
.jpg?w=400)
然后是困难的部分,在偏移的情况下将左侧缝合到右侧。

我成功了!我最终得到一个环面,由于偏移,它有一个孔。

在这一点上,理论上,我可以开始裁剪,并最终绕着整个环面进行。
.jpg?w=400)
成功了!

我很激动它成功了,但数学家很难满足。一旦我们解决了一个问题,我们就想看看是否可以简化证明或推广定理。我的斜裁滚边冒险也不例外。奇怪的环面方法很有趣,但我可以做些什么来避免沿着偏移缝合边缘吗?我可以使用一个真正的环面而不是一个奇怪的环面吗?
为了弄清楚如何解决这个问题,我必须思考一下为什么我一开始就不能缝制一个规则的环面。原因是如果我这样做,我最终会得到几个斜裁滚边环,而不是一条长条。在更深层次上,问题是斜裁滚边以相对于织物纹理成 45° 角裁剪。将织物视为一张方格纸,斜裁滚边的斜率为 1。我可以在方格纸上绘制它,方法是将顶部/底部和左侧/右侧分成相同数量的部分,然后连接这些点。我将得到与顶部和底部分割数一样多的环。
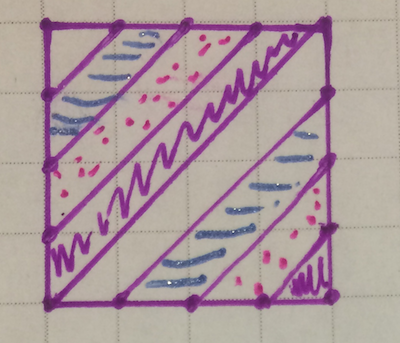
如果我将环面的顶部/底部和侧面都分成四部分,我将得到四条单独的布条。
一般来说,在环面上,如果我将顶部/底部分成m部分,并将左侧/右侧分成n部分,我将得到gcd(m,n)条单独的布条。如果 m 和 n 没有公因数,我将只得到一条布条,正如所期望的那样。
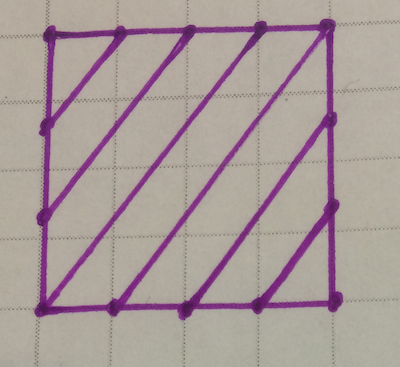
如果我将顶部/底部分成四部分,并将侧面分成三部分,我将只得到一条布条。不相信我?用您的眼睛或手指跟随这条布条。
唯一的问题是我不再制作斜裁滚边了。我正在制作非斜裁滚边。我的滚边的斜率将不再是 1,而是一些接近 1 的分数。如果我将底部分成m部分,并将侧面分成n部分,则斜率将为m/n。
现实世界有多在意我的斜裁滚边不是完全斜裁的?缝纫是一种近似的尝试,所以我认为现实世界不会太在意我的斜裁布条是否不够完美。受到鼓舞,我决定放手一搏。
我计算了数字,并确定为了获得 2 英寸宽的斜裁布条,我需要从 24 英寸的正方形布料开始,并将顶部和底部均分为九等份,并将侧面均分为八等份。然后我连接了这些点。

将布料的正面朝里,我将顶部缝合到底部,并将左侧缝合到右侧。我得到了一个环面,上面缠绕着一条长螺旋线。

然后我在上面剪了一个小孔,开始裁剪。

成功了,我最终得到一个 288 英寸长的几乎是斜裁的布料环,我将其剪开做成一条长条。我特别喜欢注意到这个小点,原始正方形的角在这里汇合在一起,并向我展示了一个小直角三角形,其直角边长之比为 8:9。在典型的斜裁滚边中,这个点将是一个等腰直角三角形。

令我惊讶的是,当我使用非斜裁滚边时,我确实注意到它感觉不如真正的斜裁滚边那么灵活。我确信,如果我在每一侧添加更多的分割,例如将斜率从 9/8 更改为 11/10 或 24/23,非斜裁滚边的作用将越来越像真正的斜裁滚边。但我的 9/8 斜裁滚边完成了这项工作。(如果我可以这么说,非常可爱。)

我的环面方法不是制作斜裁滚边的最佳方法。这项荣誉属于我最初进行实验所依据的教程。如果您只是想以一种巧妙、高效的方式制作一些斜裁滚边,您应该使用那个教程。但我的实验帮助我更深入地了解了斜裁滚边以及环面的几何形状和动力学。
这个项目也让我思考缝纫中隐藏的数学。缝纫中有很多显而易见的数学:测量布料、纸样放码、计算缝份。但缝纫中的数学远比这些技能更深入。当您深入研究时,缝纫是应用几何学。您正在使用扁平的布料来近似复杂曲面的曲率。女裁缝和其他缝纫师在应用几何学方面的研究并没有得到太多认可,这可能是因为传统上“女性化”的活动不被认为是很有数学性的。当然,我们这些缝纫或制作钩编双曲面飞机或克莱因四次曲线的人更清楚!
