本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
当我告诉人们我是数学家时,我会得到很多不同的反应。 也许令人惊讶的是,我大多得到积极的回应。 其中许多是“加油,女孩”之类的。 有些人会说,“我是[其他某种职业],但我一直喜欢数学”,或者“我希望我修过更多数学课。” 我得到一些“哇,你一定很聪明”的评论,这有点像话题终结者。 但当然,有些人告诉我他们讨厌或害怕数学。
这里有一个坦白:有时数学也让我感到害怕。 所以在万圣节,我将告诉你们一些我发现很怪异的数学:更高阶同伦群。
同伦是数学领域拓扑学中的一个基本概念,拓扑学是对形状最基本的研究。 如果你可以将一个物体拖到另一个物体上而无需切割任何东西,那么这两个物体就是同伦的。 同伦是如此基本,以至于一个空间的第一个同伦群被称为基本群。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您将有助于确保未来能够继续讲述关于塑造我们当今世界的发现和想法的具有影响力的故事。
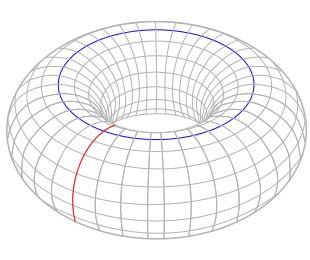
甜甜圈表面上以红色和蓝色突出显示的两条环线不是同伦的。 图片:YassineMrabet,通过 Wikimedia Commons。 CC BY-SA 3.0
基本群,或 π1,与环线的同伦有关。 我将环线想象成无限弹性的橡皮筋。 你可以做任何保持橡皮筋完整并将其留在你正在研究的表面或空间上的事情。 如果你在篮球上放两条橡皮筋,你总是可以拖动其中一条,使其与另一条对齐。 但是,如果你将一条橡皮筋绕在甜甜圈的孔上,另一条橡皮筋以另一种方式绕在孔上,你就无法将其中一条变形为另一条,而不会撕裂其中一条或离开甜甜圈的表面。 这告诉我们篮球和甜甜圈是不一样的:它们没有相同的第一个同伦群。 (以前绝对没有办法区分篮球和甜甜圈,所以我们有了拓扑学真是太好了。)
有一个关于拓扑学家的荤段子,它与“拓扑学家是无法区分结婚戒指和地上的洞,但可以区分它和地上的两个洞的人”是同伦的。 (如果你知道这个笑话,那么我的版本可能让它看起来更荤。)这个笑话是关于基本群的,它基本上告诉我们一个物体有多少个洞。
基本群一开始很难理解。 但是,如果你坐下来想象一下表面上的橡皮筋一段时间,π1 就会开始变得有意义。 然后你学习关于 同调 群。 它们有点像第一个同伦群,因为它们也测量孔洞。 有时这些孔洞是更高维度的,因此更难以可视化,但从道义上讲,它们仍然是关于孔洞的。 例如,球体没有一维孔洞——可以滑动圆圈的地方——但它有一个二维“孔洞”。 这有点让人费解,但再一次,勇敢的拓扑学学生可以适应它们。
第一个同调群通过称为 阿贝尔化 的东西与第一个同伦群相关。 阿贝尔化是什么并不太重要,但它意味着第一个同调群比第一个同伦群稍微简单一些。 这也意味着,至少对于你在基本拓扑学课程中看到的空间类型而言,第一个同伦群的描述并不比第一个同调群复杂多少。
第一个同调群和第一个同伦群之间的这种对应关系可能会让毫无戒心的拓扑学学生产生一种虚假的安全感。 因为她听说过被称为“更高阶同伦群”的东西,并假设它们一定与更高阶同调群有类似的关系。 更高阶同调群还不错,所以更高阶同伦群也不应该那么糟糕。

前方有龙。 图片:Friedrich Johann Justin Bertuch,通过 Wikimedia Commons。 PD-Art。
空间的第 n 个同伦群,称为 πn,与从 n 维球体到空间的同伦不同映射的数量有关。 (对于我们的目的,圆圈是一维球体,篮球是二维球体,依此类推。)
n 维球体是最简单的 n 维流形,因此 n 维球体的更高阶同伦群应该是理解一般更高阶同伦群的一个良好起点。 (她说道,幸福地没有意识到自己的危险。)让我们从 S2,二维球体开始。 我们已经看到 π1(S2) 是平凡的:球体上的任何环线都可以变形为任何其他环线,因此球体上只有一类环线。 为了计算 S2 的 π2,我们必须考虑我们可以用多少种不同的方式将球体“包裹”在自身周围。 如果你想象在篮球周围放一个非常有弹性的袋子,你可以将其包裹一次,或者你可以将其包裹两次、三次或任意整数次。 会有一些奇怪的地方袋子会被挤在一起,但你可以想象,一旦你将袋子包裹了几次并将其密封起来(这需要袋子自身交叉;这对我们来说不是问题),你将袋子包裹在篮球周围的次数将告诉你一些关于你拥有的地图类型的信息。 因此,S2 的第二个同伦群由整数组成。

球体上的一些点及其在霍普夫纤维化中的纤维的可视化。 图片:Niles Johnson,通过 Wikimedia Commons。 CC BY-SA 3.0。
那么 S2 的 π3 呢? 这是我的直觉失败的地方。 对于同调群,二维流形不可能有任何三维孔洞,因此对于 S2 来说,第三个同调群及以上的所有同调群都是平凡的。 我希望同伦群也是如此。 但是在 1931 年,海因茨·霍普夫发现了霍普夫纤维化,这是一个从 3 球体到 2 球体的连续函数,它与恒等映射不同伦。 因此,S2 的 π3 并不像我认为的那样平凡,而是实际上由 霍普夫纤维化 生成。
S2 的其余更高阶同伦群变得更加奇怪。 π6(S2) 是一个具有 12 个元素的循环群,这意味着存在一些从 S6 到 S2 的映射,其中执行 12 次会将你带回到与恒等同伦的东西。 π14(S2) 由一个 84 阶映射和两个 2 阶映射生成。 我起了鸡皮疙瘩,而我们才刚刚开始研究 S2!
球体的同伦群中有很多怪异的模式,所以如果你敢的话,你应该 查看它们。 我受不了鬼屋,所以我就在这里玩我的无限弹性橡皮筋。
