本文发表于《大众科学》的前博客网络,仅反映作者的观点,不一定代表《大众科学》的观点。
在本期《我最喜欢的定理》节目中,我的联合主持人凯文·克努森和我很荣幸采访了亨利·福勒。福勒博士是Diné学院数学系主任,该学院为纳瓦霍民族服务。您可以在kpknudson.com收听节目。
我在十月份的SACNAS(科学促进奇卡诺人和美国原住民协会)年度会议上见到了福勒博士。对我来说很方便的是,会议地点离我在盐湖城的家很近,骑自行车即可到达。福勒博士在会议上就他为改善纳瓦霍社区的数学教育所做的努力发表了感人的主题演讲。他参与的主要项目之一是数学圈,这是一种为初中和高中学生及其教师提供的数学强化项目。这可能会让一些播客听众和博客读者想起一些事情,因为乔治·西瑟里最近制作了一部关于这项工作的纪录片,名为《纳瓦霍数学圈》。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您将有助于确保未来能够继续发布关于塑造我们当今世界的发现和思想的有影响力的报道。
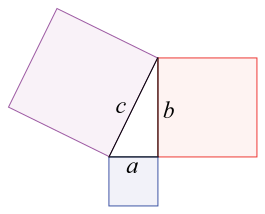
勾股定理指出,在这个边长分别为a、b和c的直角三角形中,这些边长满足关系式a2+b2=c2。在图中,蓝色和红色正方形放在一起的面积与紫色正方形的面积相同。图片来源:Wapcaplet Wikimedia(CC BY-SA 3.0)
对于他最喜欢的定理,福勒博士选择了勾股定理,这可能是数学中最著名的定理。该定理断言直角三角形的两条直角边a和b与斜边c之间的关系:a2+b2=c2。虽然现在大多数人通过希腊数学家毕达哥拉斯的名字知道它,但在毕达哥拉斯出生之前很久,包括北美在内的许多地方的人们就已经知道这些长度之间的关系。福勒博士谈到了纳瓦霍人传统上使用勾股定理的许多方面,包括距离计算、天文观测和建筑施工。
在播客的每一集中,我们都会请嘉宾将他们最喜欢的定理与某物配对:食物、饮料、艺术、音乐或生活中其他非数学的乐趣。福勒博士的定理配对有点不寻常。他谈到了勾股定理如何与他作为纳瓦霍人的传统产生交集,包括他的成长经历如何在某些方面帮助他发现自己在数学方面的天赋和兴趣。
您可以通过在本月(2017年11月;该链接可能在本月之后仍然可用)在PBS上观看纪录片来了解更多关于纳瓦霍数学圈的信息。您还可以在Zala Films网站上找到有关该纪录片的信息。
您可以在 kpknudson.com 和 Roots of Unity上找到更多关于本播客中介绍的数学家和定理的信息,以及其他令人愉悦的数学趣味内容。文字稿可在此处获取。您可以在iTunes和其他播客分发系统上订阅和评论播客。我们很乐意听取听众的意见,请发送邮件至myfavoritetheorem@gmail.com与我们联系。凯文·克努森的Twitter账号是 @niveknosdunk,我的账号是 @evelynjlamb。节目本身也有一个Twitter feed: @myfavethm 和一个 Facebook页面。请在下次加入我们,学习另一个引人入胜的数学知识。
《我最喜欢的定理》往期回顾
第0集:主持人最喜欢的定理 第1集:艾米·威尔金森最喜欢的定理 第2集:戴夫·里奇森最喜欢的定理 第3集:埃米尔·戴维·劳伦斯最喜欢的定理 第4集:乔丹·艾伦伯格最喜欢的定理 第5集:杜萨·麦克达夫最喜欢的定理 第6集:惠理子·广中(Eriko Hironaka)最喜欢的定理
