在野外遭遇组合数学

本文发表于《大众科学》的前博客网络，反映了作者的观点，不一定反映《大众科学》的观点

我最近搬家了，新家比旧家离合唱团练习的地方稍远。我走去那里的路程变长了，给了我更多的时间在漫步时沉浸在思考中。有什么比思考步行本身更好的主题呢？具体来说，作为一名数学家，我想找到我家和合唱团练习地点之间的最佳路线。

我的旧家几乎在合唱团练习地点的正北方，所以步行到那里没有太多选择。但是，新家在北方八个街区和西方六个街区。街道呈网格状，因此任何向南走八个街区，向东走六个街区的路线都可以到达合唱团练习地点。

关于支持科学新闻

如果您喜欢这篇文章，请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅，您正在帮助确保未来能够继续讲述关于塑造我们今天世界的发现和想法的具有影响力的故事。

这些路线基本上长度相同，所以我不是要尽量缩短距离。相反，我只是想找到最令人愉快的通勤方式：即遇到最少咆哮的狗，有最佳的繁忙街道交叉口，以及最美丽的风景可以在路过时欣赏。我不知道有什么捷径可以找出我的最佳通勤路线，所以我只需要尝试所有可能性。我不希望在我的路线上折返，所以我想弄清楚有多少种方法可以只向南和向东走 8 个街区向南和 6 个街区向东。

我对组合数学略知一二，组合数学是数学的一个分支，处理计算牌组、椅子上的学生，或者在我的情况下是去合唱团练习的路径的组合和排列，但我不是专家。然而，当我在最近的一次散步中思考这个问题时，我意识到它令人难忘地熟悉。事实上，几个月前我刚刚在 Project Euler 上解决了这个问题。Project Euler 是一个很棒的数学问题数据库，需要一些编程来解决。我还是编程新手，Project Euler 是我获得有趣的问题来练习和练习我的 Sage 技能的好地方。

问题 15，“网格路径”，要求我们找到在 20x20 网格中仅向下和向右移动，从左上角到右下角的不同路线的数量。

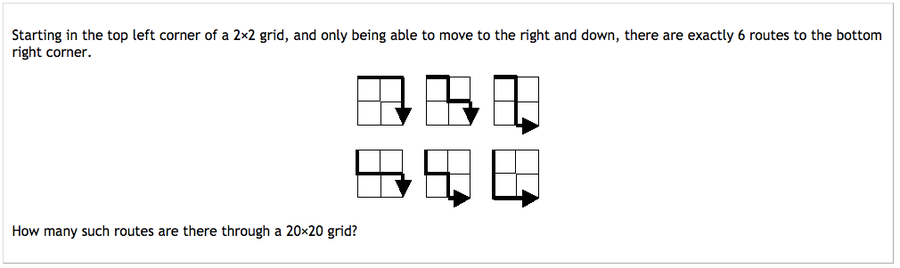
数字略有不同，但这正是我想要解决的问题，以弄清楚有多少种可能的路线可以到达合唱团练习地点。

那么答案是什么呢？好吧，Project Euler 的第一条规则是不要谈论 Project Euler。或者至少不要谈论你是如何解决 Project Euler 问题的。正如主页所说，“真正的学习是一个积极的过程，看到它是如何完成的与体验发现的顿悟相去甚远。请不要剥夺他人您自己如此珍视的东西。”

因此，我不会告诉您有多少条路径，也不会告诉您我是如何计算出来的。（如果您计算出来，请不要破坏其他人的乐趣。）但是，我要说的是，我和我的数学家配偶提出了一个详尽的解决方案，但最终远非解决此问题的最快方法。虽然当我看到更简洁的答案并意识到事后看来它是多么明显时，我感到有点傻，但我们的方法揭示了组合数学中一个新的（对我而言）恒等式。我对此真的不会生气。

我用来解决 Project Euler 问题的方法完全适用于市中心步行的情况，因此我现在知道在对哪条路线是最佳路线做出判断之前，我需要尝试多少条路线。让我们只说我有足够的

work步行任务要完成。