本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在本期《我最喜欢的定理》节目中,凯文·克努森和我很荣幸与艾米莉·戴维·劳伦斯交谈。她是旧金山大学的数学教授,研究低维拓扑学。你可以在这里或在kpknudson.com收听,那里也有本期节目的文字稿。
对于她最喜欢的定理,劳伦斯博士选择了紧曲面分类,这是拓扑学入门课程中最棒的定理之一。分类定理指出,所有满足一些温和要求的曲面都拓扑等价于球面、环面之和或射影平面之和。(碰巧的是,我之前写过关于环面的文章,一篇关于射影平面的文章也即将发布。这是一种令人愉悦的不可定向曲面,就像更强烈的莫比乌斯带。)拓扑等价允许很大的自由度。只要你可以将一个形状变形为另一个形状,而无需刺穿或粘合任何东西,这两个形状就是拓扑等价的。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于塑造我们当今世界的发现和思想的有影响力的故事。
紧曲面分类定理指出,就拓扑学而言,环面和射影平面构成除球面以外的所有其他曲面的构建块,球面只是孤立存在。如果您想知道取两个曲面的和是什么意思,这非常直观。你只需在每个曲面上切一个小孔,然后沿着孔将两个曲面缝合在一起。

两个曲面连通和过程的图示。鸣谢:Oleg Alexandrov Wikimedia (CC BY-SA 3.0)
如果你听过《我最喜欢的定理》第 0 集,劳伦斯博士最喜欢的定理听起来可能很熟悉。它与我个人最喜欢的定理,一致化定理密切相关。它们适用于略有不同的曲面类型。曲面分类定理适用于任何没有任何穿孔的二维曲面,而一致化定理仅适用于称为黎曼曲面的曲面。最重要的区别在于黎曼曲面必须是可定向的,因此一致化定理不适用于射影平面之和,而曲面分类定理对此没有问题。一致化定理不是按拓扑结构对曲面进行分类,而是说可定向曲面可以有三种不同的几何类型。它可以与曲面分类定理结合,表明每个可定向曲面都有一个自然的几何结构。像沙滩球这样没有孔洞的曲面,自然具有球面或椭圆几何。有一个孔洞的曲面自然具有平面几何,而有多个孔洞的曲面自然具有双曲几何。
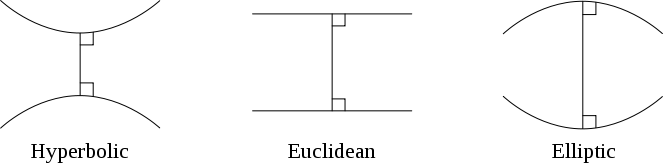
双曲几何、欧几里得几何和椭圆(或球面)几何的图示。在双曲几何中,平行线彼此远离。在欧几里得几何中,它们保持相同的距离。在椭圆几何中,没有不相交的线。鸣谢: Pbroks13 和 Joshuabowman Wikimedia (CC BY-SA 3.0)
劳伦斯博士决定用一个经典的配对来解释她的定理:甜甜圈和一杯咖啡。这指的是一个经典的数学笑话:拓扑学家是那种无法区分甜甜圈和一杯咖啡的人,因为当您拉伸或挤压表面时,它们是等价的,两者都有一个孔。

马克杯和甜甜圈拓扑等价性的演示。鸣谢:Lucas V. Barbosa Wikimedia
您可以在kpknudson.com和Roots of Unity找到更多关于本播客中介绍的数学家和定理的信息,以及其他令人愉悦的数学趣味内容。文字稿在此处可用。您可以在 iTunes 和其他播客分发系统上订阅和评论播客。我们很乐意听到听众的来信,所以请发送邮件至 myfavoritetheorem@gmail.com。凯文·克努森的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。下次加入我们,学习另一个引人入胜的数学知识。
《我最喜欢的定理》节目回顾
