本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
在本期“我最喜欢的定理”节目中,我非常荣幸地与 Dusa McDuff 本人进行了交谈!我们七月份在 MathFest,美国数学协会的年度夏季会议上见面了。第一次看到她做报告时,我太害羞了,没敢向她自我介绍,所以我很高兴这次弥补了遗憾。您可以在这里或 kpknudson.com 网站收听这期节目。
McDuff 目前是巴纳德学院的教授。在此之前,她在石溪大学工作多年。她曾获得多项重要奖项,包括 Satter 奖、高级 Berwick 奖 和 Steele 奖,并获得了多所大学的荣誉博士学位。她参加 MathFest 是为了做 Hedrick 系列讲座,并共同组织辛几何研究讨论会。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。 通过购买订阅,您将帮助确保未来能够继续报道关于塑造我们当今世界的发现和想法的具有影响力的故事。
辛几何 是复几何的近亲。这里的“复”不是指复杂,而是指复平面,一个具有实轴和虚轴的二维平面,像 2+3i 这样的复数就存在于此。复平面也有 4 维、6 维、8 维等等的版本。同样,辛几何可以存在于任何偶数维的空间中。
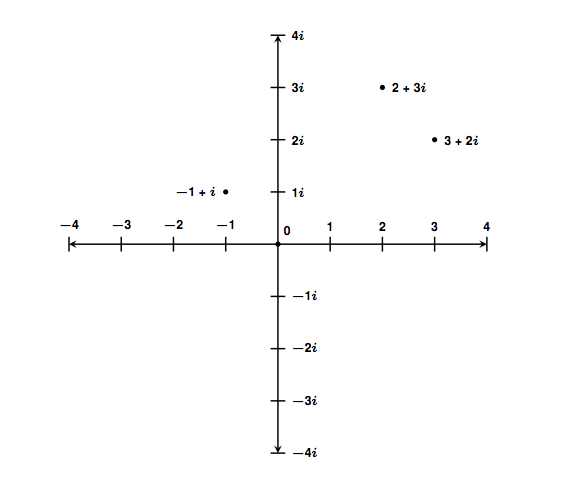
标有三个点的复平面。图片来源:Evelyn Lamb
偶数维空间上的辛结构是一种从坐标对中获取测量值的方法。例如,对于一个 4 维空间,您取两对坐标,并为每对坐标获得一个“面积”测量值。然后您将这些面积相加。正如 McDuff 在节目中所说,这看起来像是一个奇怪的选择,但最终却变成了“一件非常明智的事情”。进行这种测量的动机实际上来自于物理学,其中这两个量可以表示物体的位置和速度。
辛几何的一个研究课题是,形状的哪些变换可以保持其辛结构。McDuff 选择作为她最喜欢的定理——非挤压定理,就是这方面的一个成果。正如 Tara Holm 在这篇关于辛几何的 数学研究生水平的入门文章(pdf) 中描述的那样,非挤压定理可以被解释为:骆驼无法穿过针眼,至少只要骆驼和针是辛的。该定理由俄罗斯数学家 Mikhail Gromov 在 20 世纪 80 年代证明。
McDuff 讨论了该定理的 4 维版本:除非圆柱体的半径至少与球体的半径一样大,否则您无法在保持辛结构的同时将(4 维球体)放入(4 维)圆柱体中。四维空间很难想象,您可以想象成三维空间。(我不会告诉任何人。)在三维空间中,如果您有一个略微有弹性的球——也许是一个豆袋或篮球——您可以将其放入比球直径更窄的圆柱体中。如果球非常软——也许是橡皮泥做的——只要圆柱体足够长,您就可以通过拉伸将其放入非常细的圆柱体中。非挤压定理表明,辛结构比橡皮泥球更坚硬:即使一点点挤压,您也无法挤压它们并保持结构不变。尽管辛几何学家喜欢指出辛结构有多“柔软”,但这个定理表明,它们比体积之类的东西要坚硬得多。

为了获得最佳享受,请将非挤压定理与成熟的鳄梨搭配食用。图片来源:Andrea Pacheco Flickr(CC BY-ND 2.0)
McDuff 推荐将非挤压定理与美味的鳄梨搭配食用。您需要收听这期节目才能了解她为什么认为鳄梨是非挤压定理的完美搭配。
有关 McDuff 的更多信息,请查看 西蒙斯基金会制作的“科学人生”视频 或这篇 McDuff 在美国数学会通告九月刊上发表的关于她人生的文章(pdf)。我特别欣赏她对包括她自己在内的隐性偏见如何影响她,以及至今仍在影响数学和科学领域女性的反思。她撰写了许多关于辛几何和拓扑学的论文,包括这篇综述文章“什么是辛几何?”。对于具有高等数学背景的人来说,这是一篇很好的入门介绍。
您可以在 kpknudson.com 和 “单位根” 博客上找到更多关于本播客中介绍的数学家和定理的信息,以及其他令人愉悦的数学趣闻。 节目文字稿可在此处获取。您可以在 iTunes 和其他播客分发系统上 订阅和评论播客。我们很乐意听到听众的反馈,请发送邮件至 myfavoritetheorem@gmail.com 联系我们。Kevin Knudson 的 Twitter 账号是 @niveknosdunk,我的账号是 @evelynjlamb。该节目本身也有一个 Twitter 账号:@myfavethm 和一个 Facebook 页面。请在下期节目中加入我们,了解另一个引人入胜的数学知识。
“我最喜欢的定理”节目往期回顾
第 0 集:主持人最喜欢的定理 第 1 集:Amie Wilkinson 最喜欢的定理 第 2 集:Dave Richeson 最喜欢的定理 第 3 集:Emille Davie Lawrence 最喜欢的定理 第 4 集:Jordan Ellenberg 最喜欢的定理
