本文发表在《大众科学》的前博客网络中,反映了作者的观点,不一定代表《大众科学》的观点
背诵圆周率数字的比赛是一个非常常见的圆周率日活动。而今年恰逢百年一遇的月份/日期/年份与圆周率的前几位小数数字相吻合,我们可能会遇到比平时更多的这类活动。我们有10根手指,这使得十进制数字成为自然的选择,但如果我们是水豚或者辛普森一家,我们可能会使用8进制。如果我们是古代美索不达米亚人,我们会使用60进制。记忆任何这些进制下的数字都有点随意。圆周率的十进制、八进制和六十进制数字并不能捕捉到圆周率的真正本质。为什么不举办一个既有背诵十进制数字的乐趣,又没有任意进制依赖的比赛呢?没错,今年你需要举办一个连分数背诵比赛!
“听起来不错,”我似乎听到你在说,“但那是什么意思?”很高兴你问了!几年前,我写了一篇关于连分数的博客,这是表示数字最浪漫的方式。正如我当时写的那样,连分数就像分数,但更进一步。它不是在分子和分母中各有一个数字就停止了,而是分母中也有一个分数。而那个分数的分母中也有一个分数,以此类推。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过
订阅来支持我们屡获殊荣的新闻报道。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
为了标准化连分数,我们要求每个分子都为 1,每个分母都为正数。(我们也允许自己在连分数的前面添加一个任意的正或负整数,这样我们就可以表示不在 0 和 1 之间的数字。)
有了这些限制,每个数字都有一个(基本上)唯一的连分数表示形式。如果这个数字是有理数,那么连分数最终会终止。如果它是无理数,那么连分数就会无限继续下去。
虽然我们使用十进制记数法来书写连分数的分母,但连分数不依赖于进制。12 这个数字,无论我们把它写成 10 进制的 12、2 进制的 1100 还是 16 进制的 C,都是相同的数字。所以,如果 12 出现在连分数的分母中,那么用什么进制来写它都无关紧要。一个数字的连分数表示形式,无论我们使用什么进制,其中的数字都相同,可能只是写法不同而已。
一个数字 x 的连分数展开式告诉我们哪些有理数或分数是对 x 的最佳近似值。当我们在一定数量的项之后截断连分数时,我们得到所谓的 x 的收敛项。如果收敛项的分母为 n,则表示没有比 n 小的分母更接近 x 的数字。收敛项在更强的意义上是最佳近似值,但那是另一个话题。总之,可以说收敛项是最佳近似值中的最佳值,是近似值中的精华。
举一个具体的例子,让我们看看圆周率这个数字。圆周率的连分数是
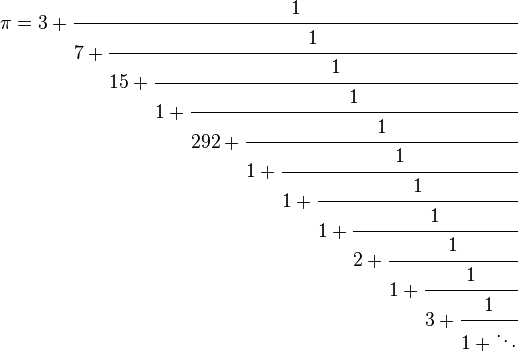
圆周率的连分数展开式。
而前几个收敛项是:3(当然),22/7(圆周率近似日),333/106,355/113 和 103,993/33,102。在 22/7 之后,所有的收敛项都比 3.1415(与今年的圆周率日日期相对应)更好地近似圆周率。事实上,355/113 的精度比 3.1415 高出两位小数,而分母中只有三位数,而不是五位数(如果您将 3.1415 视为 31,415/10,000)。如此高效,为什么还要费心使用十进制数字呢?当其他人在庆祝“我们一生中唯一的圆周率日”时,你应该告诉他们 3.1415 不是对圆周率的一个很好的近似值。尽量避免在 9:26 说这句话。

索伊德伯格也同意:3.1415 不是圆周率的最佳近似值。图片由我本人在 memegenerator.net 制作。
背诵连分数比背诵十进制数字是更好的庆祝圆周率的方式。你不会把时间浪费在对应于圆周率平庸近似值的数字上,而只会提到对应于圆周率真正良好近似值的数字。最大的难题是你应该背诵连分数中的分母列表(整数数列在线百科全书中的数列 A001203)还是其收敛项,也就是最能近似圆周率的分数本身。收敛项有点棘手:分子在整数数列 A002485 中,分母在数列 A002486 中。背诵连分数的分母更类似于数字背诵比赛,但收敛项提供了更大的挑战!
我必须指出,除了十进制是表示圆周率的一种任意方式之外,我不喜欢数字背诵比赛的原因之一是,借用我从某处读到的一个比喻,记忆圆周率的数字之于数学,就像记忆罗伯特·弗罗斯特诗歌中的字母顺序之于文学。这不是一项具有智力意义的活动。在这方面,连分数背诵比赛并不比数字背诵比赛好。如果您想用更具数学本质的活动来庆祝圆周率日,请查看去年圆周率日关于 Math Munch 的文章,其中包含使用蒲丰投针或观看 Aperiodical 的好心人制作的这个有趣的视频来估计圆周率的说明,其中几位数学家采用了各种圆周率近似策略,但结果好坏参半。或者阅读我去年关于 π(x)(素数计数函数,π 符号的另一种数学用法)的文章。无论你做什么,祝你圆周率日快乐!

