本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点。
本月早些时候发布的 Numberphile视频 声称所有正整数的和为 -1/12。
我通常是 Numberphile 团队的粉丝,他们出色地使数学变得令人兴奋和易于理解,但这个视频让我感到失望。将数字 -1/12 与级数 1+2+3+4... 联系起来是有意义的方法,但在我看来,称其为级数的和是具有误导性的。此外,它的呈现方式助长了我作为数学教育者经常遇到的一个误解,即数学家们在毫无明显理由的情况下武断地改变规则,学生们对在特定情况下什么是允许的,什么是不允许的,没有任何希望了解。在关于这个视频的一篇文章中,物理学家 Dr. Skyskull 说,“令人沮丧的是,很大一部分人自动认为数学是一些非直观的、奇异的巫术,只有超级智能的人才能理解。在没有任何限定的情况下展示这样一个疯狂的结果只会加强这种观点,而且在我看来,这对数学是一种损害。”
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道: 订阅。通过购买订阅,您正在帮助确保关于塑造我们今天世界的发现和想法的有影响力的故事的未来。
加法是一种二元运算。你输入两个数字,然后得到一个数字。但你可以将其扩展到更多数字。例如,如果您有三个数字要相加,您可以先将其中任意两个数字相加,然后将第三个数字加到结果和中。我们可以对任意有限数量的加数重复此操作(算术定律表明,无论我们以什么顺序相加,我们都会得到相同的答案),但是当我们尝试将无限数量的项相加时,我们必须选择加法的含义。处理无限加法最常见的方法是使用极限的概念。
粗略地说,我们说如果当我们添加越来越多的项时,我们越来越接近数字 L,那么无穷级数的和就是一个数字 L。如果 L 是有限的,我们称该级数为收敛级数。收敛级数的一个例子是 1/2+1/4+1/8+1/16…。这个级数收敛于数字 1。很容易看出原因:在第一项之后,我们离 1 还差一半。在第二项之后,我们离 1 还差剩余距离的一半,依此类推。
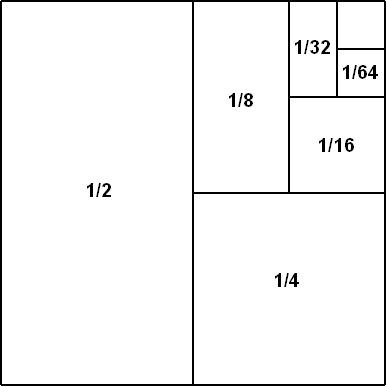
1/2+1/4+1/8...=1 的可视化“证明”。图片来源:Hyacinth,通过 Wikimedia Commons。
芝诺悖论 说我们永远不会真正达到 1,但从极限的角度来看,我们可以尽可能接近我们想要的。这就是数学家在谈论无穷级数时通常所说的“和”的定义,它基本上符合我们对“和”和“等于”这两个词的直观定义。
但并非每个级数在这种意义上都是收敛的(我们将非收敛级数称为发散级数)。有些级数,如 1-1+1-1…,可能会在我们不断添加更多项时在不同的值之间跳动,而有些级数,如 1+2+3+4...,可能会变得任意大。很明显,那么,使用级数收敛的极限定义,级数 1+2+3… 不收敛。如果我说,“我认为这个级数的极限是某个有限数 L,”我可以很容易地计算出要加多少项才能达到我想要的数字 L 以上的程度。
将数字 -1/12 与级数 1+2+3... 联系起来是有意义的方法,但我更愿意不将 -1/12 称为正整数的“和”。解决这个问题的一种方法是使用复分析中的解析延拓的思想。
假设您有一个函数 f(z),它定义在复平面中的某个地方。我们将函数定义的域称为 U。您可能会找到一种方法来构造另一个函数 F(z),该函数定义在更大的区域中,使得当 z 在 U 中时,f(z)=F(z)。因此,新函数 F(z) 在 f(z) 定义的任何地方都与原始函数 f(z) 一致,并且它在 f(z) 域外的一些点处定义。函数 F(z) 称为 f(z) 的解析延拓。(“The”是合适的冠词,因为函数的解析延拓是唯一的。)
解析延拓很有用,因为复函数通常定义为涉及变量 z 的无穷级数。然而,大多数无穷级数仅对 z 的某些值收敛,如果我们能让函数在更多地方定义,那就太好了。函数的解析延拓可以为函数定义在其无穷级数定义收敛区域之外的值。我们可以通过将函数的解析延拓追溯应用到其原始无穷级数定义来说 1+2+3...=-1/12,这种做法应该伴随着 Lucille Bluth 式的眨眼。

问题中的函数是黎曼 zeta 函数,它以其与关于素数分布的问题的深刻联系而闻名。当 s 的实部大于 1 时,黎曼 zeta 函数 ζ(s) 定义为 Σ∞n=1n-s。(我们通常使用字母 z 作为复函数中的变量。在这种情况下,我们使用 s 是为了尊重黎曼,他在 1859 年的论文 [pdf] 中定义了 zeta 函数。)当 s=-1 时,这个无穷级数不收敛,但你可以看到,当我们代入 s=-1 时,我们得到 1+2+3…。黎曼 zeta 函数是此函数到整个复平面减去点 s=1 的解析延拓。当 s=-1 时,ζ(s)=-1/12。通过在 ζ(-1) 和在复平面的其他部分定义该函数的正式无穷级数之间放一个等号,我们得到 1+2+3...=-1/12 的陈述。

解析延拓不是将数字 -1/12 与级数 1+2+3... 联系起来的唯一方法。有关一种不需要复分析的方法的非常好的、深入的解释(包括家庭作业练习),请查看 Terry Tao 关于这个主题的帖子。
Numberphile 视频让我感到困扰,因为他们有机会谈论为无穷级数赋值的意义,并解释不同的方法。如果您已经对该主题有所了解,您可以观看该视频和关于该主题的更长的相关视频,并了解真正发生的事情的片段。但是,如果观众认为“和”的含义与他们认为的含义相同,那么对于一堆正数加起来等于一个负数来说,视频的“哇”因素就来自于它毫无意义的事实。
.jpg?w=350)
通过 quickmeme。
如果 Numberphile 团队更明确地说明将数字与级数关联的替代方法,他们本可以做的不仅仅是让人认为数学家总是在改变规则。在视频的结尾,制片人 Brady Haran 问物理学家 Tony Padilla,如果他在计算器上永远添加整数,最后按下“等于”按钮,是否会得到 -1/12。Padilla 厚颜无耻地说,“你必须达到无穷大,Brady!” 但答案应该是“不!” 在这里,我认为他们错过了一个机会来澄清他们正在使用一种为无穷级数赋值的替代方法,这将使视频的误导性大大降低。
其他人已经写了一些关于这个视频中数学的好东西。在 Slate 博客文章 对此过度轻信之后,Phil Plait 写了一篇更加冷静的解释,解释了为级数赋值的不同方法。如果您想自己研究“证明”的细节,John Baez 已经为您准备好了。Blake Stacey 和 Dr. Skyskull 写了关于用数字 -1/12 代替正整数的和在物理学中如何有用的文章。Richard Elwes 发布了一个无穷级数“健康和安全警告”,其中涉及我最喜欢的调和级数。我认为关于这个无穷级数意味着什么的大量讨论是好的,即使我希望更多的讨论可以在视频中进行,到目前为止,该视频在 YouTube 上的观看次数已超过一百万次!