本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点。
几年前,当弗兰克·法里斯在联合数学会议上谈论他的艺术展览 《看见对称》时,我第一次听说他的作品,并立刻被迷住了。不久之后,我读到了他的“不可能的壁纸”,它似乎具有数学上不可能的五重旋转对称性。现在他出版了一本关于他作品的书,《创造对称:壁纸图案的巧妙数学》。这本书是一本精美的图文指南,旨在融合数学和艺术创造力,以生成引人入胜且视觉上吸引人的设计。
《创造对称》涵盖了与对称性相关的数学的几个不同方面。 广义上讲,法里斯从曲线的对称性开始,转移到欧几里得平面中的对称性,最后探索球面几何和双曲几何中类似的对称性。 在数学上,本书结合了复分析、傅里叶级数、抽象代数和现代几何。 虽然这个列表看起来令人生畏,但没有任何先决条件。 这些解释是独立的且清晰的。
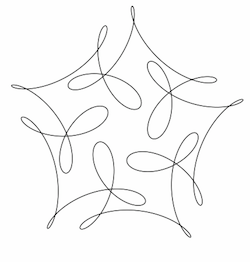
弗兰克·法里斯的“神秘曲线”。 公式为 µ(t)=(cos(t)+cos(6t)/2+sin(14t)/3, sin(t)+sin(6t)/2+cos(14t)/3)。 五重对称性从何而来? 图片:弗兰克·法里斯,©普林斯顿大学出版社。经许可使用。
关于支持科学新闻业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻业 订阅。 通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
第一章向我们介绍了一条诱人的“神秘曲线”。 神秘之处不在于曲线的公式,而在于它为什么看起来是这个样子。 该函数是正弦和余弦的组合,其中有很多 6 和 14 在浮动,但不知何故它具有五重旋转对称性。 “花点时间用你的眼睛追踪它,欣赏它舞动的起伏,”法里斯写道。 “我希望这个图形——‘神秘曲线’——会让你感到惊讶。” 这条曲线提供了深入研究三角函数组合中的系数如何影响结果曲线外观的动力。 (有关此类曲线的更多信息,包括交互式曲线生成器,请参阅 Mike Croucher 的帖子,灵感来自法里斯和 John D. Cook。)
正如神秘曲线的情况一样,可视化贯穿本书始终推动着数学的发展。 在一章中,法里斯写道,
在研究壁纸函数多年后,当我以为至少从数学的角度来看,这个故事不可能再添加任何东西时,我的屏幕上出现了一张图像。 我称之为“快乐的意外时刻”,因为随机选择的壁纸系数导致了一些我认为可以构成一个相当好的故事的东西。
像这样的“快乐的意外”在书中多次出现,它们帮助读者理解对于法里斯来说,数学和艺术的创造力如何相互促进。
本书的大部分内容致力于壁纸群和饰带群。 壁纸群描述了在平面中两个方向上具有对称性的图案,而饰带群描述了在一个方向上具有对称性的图案。 这些群组是很有吸引力的主题,有很多方法可以了解它们,从代数教科书到 YouTube 视频。
.jpg?w=300)
山峰上的桃子及其负片为帖子顶部的变形饰带和下方的双曲壁纸创建了“色轮”。 图片:弗兰克·法里斯,©普林斯顿大学出版社。经许可使用。
对我来说,《创造对称》与众不同之处主要有两点。 首先是如何无缝地将几何和代数结合起来描述这些图案。 第二是颜色。 可视化平面的变换可能很困难,因为这种变换的“图表”将存在于四维空间中。 解决这个问题的一种常见方法是以某种方式为平面着色,并显示变换“之前”和“之后”的图片。 (有关此方法的美丽示例,请参阅关于莫比乌斯变换的这段视频。)法里斯接受了这个想法并加以应用。 法里斯没有使用简单的色轮或正方形网格,而是使用了他自己的照片,或者正如他所描述的那样,“世界是我的色轮”。
.jpg?w=300)
由上面的 Kaiser Peach 色轮制成的双曲壁纸图案。 图片:弗兰克·法里斯,©普林斯顿大学出版社。经许可使用。
法里斯为函数着色的方法使数学和艺术之间的竞争环境趋于平等。 法里斯不仅仅使用颜色来说明数学函数,他还使用数学将风景、花卉或晚餐的快照转化为美丽的设计。 数学和设计是平等的伙伴。 法里斯多次使用一些相同的色轮,看到从一个来源可以涌现出多少不同的图案,这真是令人着迷。 我最喜欢的色轮是Kaiser Peach,如上图所示,部分原因是它的故事。 法里斯写道:“攀登内华达山脉的凯撒峰是一个受欢迎的朝圣之旅,带一个桃子到山顶是一种使桃子味道特别美妙的传统方式。”
法里斯的色轮激发了他超越 17 个壁纸群和 7 个饰带群。 通过创建由图像及其负片组成的色轮,旋转 180 度,他引入了颜色反转对称性。 顾名思义,在这些对称性中,图像的变换最终使形状保持不变,颜色切换为其负片。 通过使用颜色的“旋转”而不是负片,他将这个想法进一步推广到“颜色旋转”对称性,例如,平面的三重旋转将橙色变为紫色,紫色变为绿色,绿色变为橙色。
《创造对称》是为谁而写的? 这本书不是典型的流行数学读物。 它包含大量的方程式和技术细节,我可以看到它在几种不同的情况下可以作为教科书发挥作用:作为复分析或抽象代数的补充,或者作为不寻常的本科数学选修课的组织框架,可以更深入地研究每个主题。 但是,尽管这本书可以作为教科书,但它仍然温暖而友好,没有高等数学背景的人也可以欣赏它,只要他们不介意跳过一些明确标记的技术部分。 法里斯的善良、热情和略带古怪的幽默感(例如,他透露他会暂停电影来检查背景中壁纸的对称群)使原本可能枯燥的主题变得引人入胜。 到最后,您可能已准备好为自己创造对称性。
