本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
海豚的三角剖分。图片来源:Crhschn,通过维基共享资源。
曲面是复杂的。三角形是简单的。这是创建计算机图形和一些高等数学背后的一种思想。如果我们有一个曲面,我们可以取曲面上的一堆点,并将它们连接成三角形,以获得曲面的近似值。这很好,但是三角剖分有多可靠?它在多大程度上反映了原始曲面的属性?例如,当我们增加曲面近似值中三角形的数量时,三角剖分曲面的表面积会接近原始曲面的表面积吗?

卡尔·赫尔曼·阿曼杜斯·施瓦茨,他是第一个描述施瓦茨灯笼的人。图片来源:公共领域,通过维基共享资源。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
1880年,数学家和正义的胡须维护者赫尔曼·施瓦茨通过产生一个反例,一个曲面和一系列三角剖分近似值,否定地回答了这个问题,对于这些近似值,三角剖分的表面积变得任意大,因此不收敛到原始曲面的表面积。
本学期早些时候,我有机会参加当地女性数学协会分会举办的折纸工作坊。拉迪卡·古普塔是犹他大学的研究生,她向我们展示了如何仅通过折叠纸张来制作这个被称为施瓦茨灯笼的反例。
要制作施瓦茨灯笼,我们从一张纸开始。
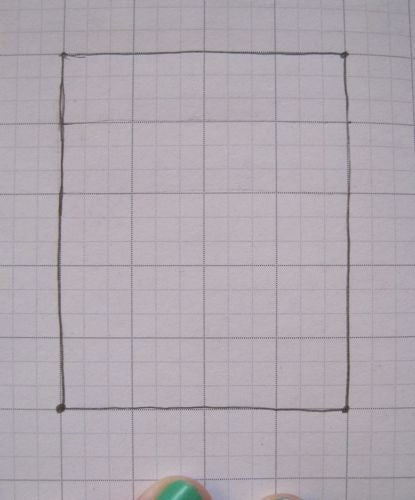
图片来源:伊芙琳·兰姆。
我们将纸张的长度分成 M 部分,这样我们就得到了 M 个细长的水平矩形。
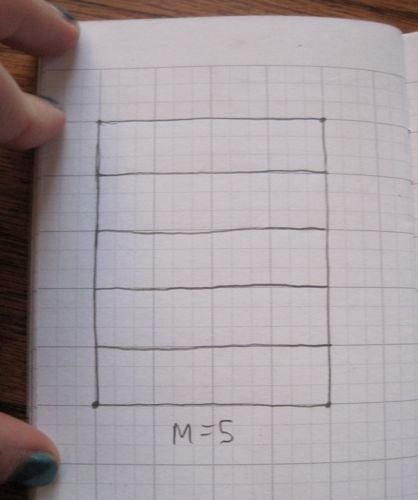
图片来源:伊芙琳·兰姆。
然后,每个细长的水平矩形通过在顶部和底部以偏移量放置 N 个点并将这些点连接成三角形,从而分成 2N 个三角形。(请注意,最后,左右两侧将粘合在一起,因此绘制了一些三角形,以便在粘合前一半在右侧,一半在左侧。)
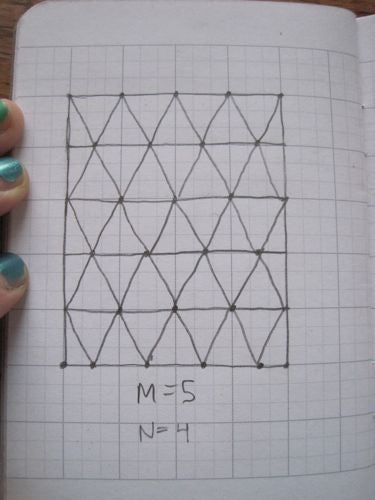
图片来源:伊芙琳·兰姆。
现在我们只需要将水平线“向内”折叠,将对角线“向外”折叠,并将右侧粘贴到左侧,以获得一个由三角形面组成但看起来有点像圆柱体的表面。(注意:此步骤有点困难。我不得不向工作坊负责人古普塔和我的一个学生寻求帮助,他是一位才华横溢的折纸爱好者。您可能也需要帮助。)

我和我的朋友们一起制作的施瓦茨灯笼。顶点(尖点)都位于圆柱体上。(这不是用前三张图片中的纸张制作的。它比那张纸张有更多的三角形。)图片来源:伊芙琳·兰姆。
随着 M 和 N 的增加,三角剖分在某种意义上收敛到圆柱体:随着三角形数量的增加,三角剖分上任何点与圆柱体上点之间的距离趋于 0。但是,根据 N 与 M 的比率,三角剖分的表面积可能不会收敛到圆柱体的表面积。如果 N 比 M 大得多(特别是,如果比率 N/M 不趋于 0),则三角剖分的表面积会变得任意大。另一种思考方式是,如果 N 相对于 M 非常大,那么随着 N 和 M 的增加,当您将它们折叠起来时,得到的圆柱体就会越来越小。
值得问一下,我们是否应该对能够创建这个反例感到惊讶。我们应该期望曲面的三角剖分近似值具有与曲面本身相同的属性吗?当我在尝试决定施瓦茨灯笼是令人震惊还是仅仅有趣时,我想到了当我们提出关于平面曲线的类似问题时会发生什么。当我们用多边形(具有直边的形状)近似平面中的弯曲形状时,多边形的周长会收敛到弯曲形状的周长吗?不一定。让我们只考虑一个圆作为我们要近似的形状。如果我们限制我们的近似值为正凸多边形(您的标准等边三角形、正方形等),那么我们可以通过增加正多边形的边数来近似圆。在这种情况下,随着边数的增加,多边形的周长确实会趋于圆的周长。但是,如果我们放宽规则,则可以绘制一系列看起来收敛到圆但其周长始终顽固地等于 4 的多边形。有关该构造的精彩解释,请参阅 Vi Hart 的视频π=4 的证明狂想曲。虽然这不是一个完美的类比,但我认为施瓦茨灯笼的想法与该视频中的想法相似,因此在某种意义上,它的存在并不太令人惊讶。
有关施瓦茨灯笼的更多信息,请查看Conan Wu 的博客文章或其在Cut the Knot上的页面。Wu 的帖子包括一个可打印的模板和制作您自己的说明!

从上方看到的施瓦茨灯笼。图片来源:伊芙琳·兰姆。