本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定代表《大众科学》的观点
2003 年,当我还是大学二年级学生时,我很高兴地越来越深入地研究音乐理论和数学。为了配合我的个人风格,我为 20 世纪音乐课的作业写了一个 12 音序列,以表达微积分基本定理的一个陈述。
正如 Vi Hart 在下面的精彩视频中所解释的那样,12 音序列主义是在 20 世纪初提出的,目的是鼓励作曲家摆脱传统的调性,创作出没有任何音符比其他音符更重要的音乐。
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关当今世界发现和塑造我们世界的具有影响力的故事的未来。
序列作曲家从一个音列开始,该音列是八度音阶中十二个半音(或 12 个钢琴琴键:C-C#-D-D#-E-F-F#-G-G#-A-A#)的排序。
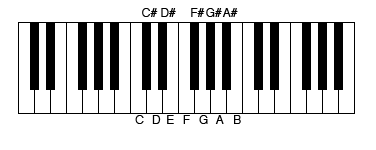
一个键盘草图,显示构成 12 音音列中音符的 12 个音高。来源:Evelyn Lamb,基于Spindoktoren Wikimedia (CC BY-SA 3.0)
我在我的作品中使用的音列是 F#-A-E-D-C#-F-B-G-G#-A#-D#-C。

我的音列,记在五线谱上。来源:Evelyn Lamb
该音列及其某些修改形式,例如将音列移调到不同的音符开始或倒退演奏,提供了作品中允许的材料。作曲家必须按照顺序使用这些音列中的音高(在任何八度音阶中),然后再重复使用较早的音高。(一些作曲家对规则的解释略有不同,但这就是要点。)这是我的歌曲中人声部分的第一行。
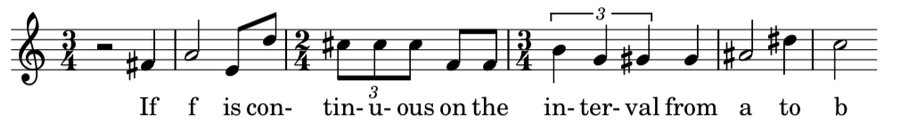
来源:Evelyn Lamb
我的作品绝非天才之作(要聆听 12 音序列天才之作,请查看 Alban Berg 的抒情组曲),但如果我这么说,我的音列还是很棒的。开头和结尾的四音组让人想起传统的调性,但整个音列足够崎岖,足以让事情变得有趣。但我特别自豪于音列的另一个特点:就像《抒情组曲》中的主要音列之一一样,它包含 12 音系统中两个音符之间所有可能的音程。(逻辑上来说,这样的音列被称为全音程音列。)
如果您还不熟悉音乐音程的名称,这没什么大不了的。如果您可以想象在钢琴上弹奏音符,您可以计算钢琴琴键,以半音为单位告诉您音程。我的音列中的第一个音程 F#-A,是一个升小三度或一个降大六度,这取决于作曲家选择 A 比 F# 高还是低。为了实用起见,我将始终参考音程升序版本的半音数,因此 F#-A 是 3 个半音的音程。音列中的下一个音程 A-E 是一个升纯五度,7 个半音。音程 E-D 是 10 个半音,依此类推。我的音列中完整的音程序列是 3-7-10-11-8-6-1-2-5-9。两个连续音高之间的每个音程都不同,这意味着从 1 到 11 的每个可能音程都出现在其中某个位置。
我为找到这个全音程音列感到自豪,这一发现让我想找到更多的全音程音列并弄清楚如何描述它们。最终,我开始注意到我找到的音列中的一些常数:三全音(6 个半音的音程,在我的音列中,在 F 和 B 之间)总是正好在中间,并且音程具有很好的对称性。第一个音程是 12 减去最后一个音程,第二个音程是 12 减去倒数第二个音程,依此类推。考虑此属性的另一种方法是,倒退演奏的音列与原始版本的音列具有相同的音程。
注意到这些模式后,我开始尝试从数学上证明每个全音程音列都必须具有相同的属性。我一直被卡住。诚然,我当时在数学上并不特别精通。我刚刚开始上一门证明入门课,我的数学技能更多的是计算而不是理论。但我缺乏精通,我用时间来弥补。我花了很多时间在这个问题上,但毫无进展。最终我继续我的生活,但这个问题一直困扰着我。多年来,每当我有纸并且非常不想做当时我应该做的事情时,我都会时不时地回到这个问题上。仍然一无所获。
最终,几年前,我决定放弃并看看是否有人为我证明了这个定理。令我震惊的是,我发现这个问题在 1965 年就已被研究过,我错了!(我忘记了尝试证明定理的关键部分:你应该花一部分时间尝试反驳它!)在《新音乐的视角》一篇名为“关于十一音程十二音列”的论文中,Stefan Bauer-Mengelberg 和 Melvin Ferentz 详细描述了他们通过计算机辅助枚举全音程音列的路径。
这篇论文有一些可爱的小细节。在脚注中,作者描述了一些熟悉的感受
通过消除以外的程序获得音程音列的问题已被证明具有高度传染性,在整个 1963 年,作者和他们的许多同事一直在相互再感染。在他们发烧的状态下,他们提出了许多假设,但大多数都被证明是错误的……
得知他们的两个假设与我的假设相同,我感到很欣慰:一个全音程音列在正向或反向阅读时具有相同的音程,并且三全音将在中间。(他们写了前一个猜想,“支持它的有力证据是 [作曲家和音乐理论家] Milton Babbitt 无法立即提出反例。”)但研究这个问题的 IBM 研究人员给了他们两个反例
C-B-D#-F-G#-C#-G-E-D-A-A#-F#

一个反例音列。来源:Evelyn Lamb
C-D#-E-A-B-A#-G#-F-C#-G-D-F#

第二个反例,粉碎了我所有的伟大梦想。来源:Evelyn Lamb
在第一个反例中,三全音(C# 和 G 之间)在音列的中间;在第二个反例中,三全音(也在 C# 和 G 之间)是倒数第三个音程。
Bauer-Mengelberg 和 Ferentz 将音乐条件转化为关于排列的数学问题,并编写了一个计算机程序来查找可以生成全音程音列的所有排列。在 IBM 7094 上运行七分十二秒后,有 1,928 个这样的排列,每个排列都可以用来创建 24 个不同的全音程音列,总共有 46,272 个全音程音列,而在 479,001,600 个可能的音列中,大约是 1/10,000(巧合的是,与一个有 14 个孩子的家庭全部生男孩的几率相似)。
Bauer-Mengelberg 和 Ferentz 希望找到简单的数学条件,使其能够找到并描述所有全音程音列。相反,在进行一些基本的简化之后,他们找到音列的方法归结为蛮力,列出可能的排列并剔除不具有所需属性的排列。这种缺乏结果让他们感到值得注意。他们写道:“事实上,迄今为止获得的最有趣的结果也许是,这些结构的数学特征,正如我们将看到的那样,非常简单,但在某些方面却如此难以分析。”我很高兴不仅是我一个人!
后来的研究,包括 Robert Morris 和 Daniel Starr 的“全音程系列的结构”,提供了一些分类和生成全音程音列的替代方法,但它们仍然有些神秘。没有容易让人类执行的生成它们的配方,并且它们并非都具有相同的属性。我很欣慰,我终于在我对全音程音列进行数学描述的探索中找到了答案,即使这是因为我错了。
