本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
欧几里得几何,大约在公元前300年由亚历山大的欧几里得在历史上最具影响力的教科书之一中编纂而成,它基于23个定义、5个公设和5个公理,或“公认概念”。但正如我在我最近关于双曲几何的帖子中提到的,其中一个公设,即平行公设,与其他公设不同。
在托马斯·希思对欧几里得《几何原本》的翻译(也称为我所拥有的译本)中,五个公设被表述为
“设以下为公设
1)从任意点到任意点可以作直线。
2)有限直线可以沿直线无限延长。
3)以任意点为圆心,任意长为半径,可作圆。
4)所有直角都彼此相等。
5)如果一条直线与两条直线相交,且在同一侧的内角之和小于两个直角,则这两条直线无限延长后,在内角和小于两个直角的一侧相交。”
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保未来继续有关于塑造我们当今世界的发现和思想的具有影响力的报道。
前四个简短明了,但第五个却很冗长。在图片中更容易理解。
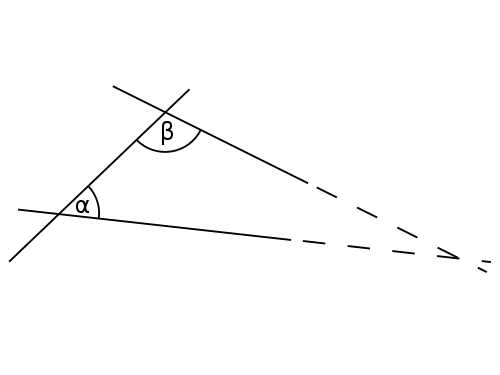
平行公设指出,如果角 α 和 β 的度数之和小于 180 度,则虚线最终会相交。图片来源:6054,来自 Wikimedia Commons。CC BY-SA 3.0。
平行公设似乎很自然,但它是一种似乎应该是定理的陈述——我们可以使用其他公理和公设来证明的东西——而不是公设。 2000年来,数学家们试图证明这一点,以表明平行公设可以从其他公理和公设中推导出来。(关于试图这样做的数学家之一乔瓦尼·吉罗拉莫·萨切里的精彩故事,请查看托尼·克里斯蒂的博客文章平行线的问题。)
每一次尝试将平行公设作为定理证明的努力都注定要失败,因为平行公设独立于其他公理和公设。我们可以不使用平行公设,或者使用不同版本的公设来构建几何,使其符合所有其他公理。双曲几何,我上一篇文章的主题,使用了不同版本的平行公设,因此最终得到了一个完全不同的几何形状。
我不是数学史学家,所以我对试图证明平行公设的感受的想法是推测性的。但我将平行公设想象成床单上的皱纹,当你试图抚平它时,它会移动,但永远不会消失。人们试图通过证明平行公设来“抚平”它,但他们只是将皱纹推到了其他陈述中。这些陈述对我来说很着迷。它们中的任何一个都可以取代平行公设,但与平行公设一样,它们不能仅使用其他公设和公理来证明。
普莱费尔公理可能是与平行公设等价的最简单的陈述。事实上,我学到它时就把它当作平行公设:在平面上,给定一条直线和一个不在该直线上的点,通过该点只能作一条与已知直线平行的直线。
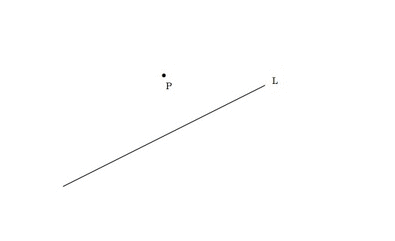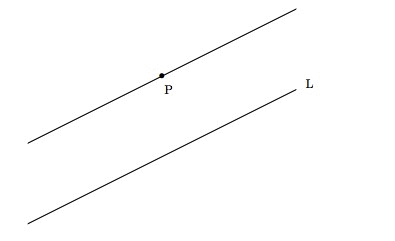
普莱费尔公理指出,通过点 P 只有一条直线不与直线 L 相交。图片来源:伊芙琳·兰姆。
普莱费尔公理简单而直接,但一些与平行公设等价的最有趣的陈述涉及三角形。您可能还记得高中几何课上三角形的角之和为 180 度。这只有在您假设平行公设的情况下才成立。事实上,它等价于平行公设。但是等等,还有更多:所有三角形的角之和都相同的陈述也等价于平行公设。我认为这很吸引人,因为这意味着在其他几何形状中,存在内角和不同的三角形!例如,在双曲几何中,角之和可以是小于 180 度且大于或等于 0 度的任何数字。

这些双曲三角形的角之和为 0 度。图片来源:Saric,来自 Wikimedia Commons。
不难看出,不同几何形状中三角形的性质会导致其他形状的性质。例如,欧几里得几何是唯一具有矩形的几何形状。为什么?如果您通过绘制对角线将矩形分成两个三角形,您最终会得到两个全等三角形。矩形的角之和为 360 度,因此每个三角形的角之和必须为 180 度。如果您喜欢矩形,请坚持使用欧几里得几何。

如果您想再次看到这些,您最好接受平行公设。图片来源:Webber,来自 Wikimedia Commons。
回到三角形,您可能还记得“相似”三角形和“全等”三角形的概念。如果两个三角形具有相同的角,则它们是相似的;如果它们相似且具有相同的边长,则它们是全等的。

相似但不全等的欧几里得三角形。相似但不全等三角形的存在等价于平行公设。图片来源:Nguyenthephuc,来自 Wikimedia Commons。
在欧几里得几何中,存在相似但不全等的三角形。事实上,有很多这样的三角形。无论您从哪个三角形开始,您都可以将其放大或缩小到您想要的任何尺寸。然而,存在相似但不全等三角形这一事实非常特殊。这是又一个等价于平行公设的陈述!例如,在双曲几何中,三角形的角唯一地确定了其边长。这有一个更令人惊讶的后果:欧几里得几何是唯一三角形可以任意大的几何形状。在双曲几何中,存在最大的三角形。
另一个关于三角形的且与平行公设等价的陈述是勾股定理:在直角三角形中,斜边长度的平方等于另外两条边长度的平方和。它是我们在几何学中学到的最早的定理之一,但只有在我们假设平行公设的情况下才成立。

奥利弗·伯恩 1847 年翻译的欧几里得《几何原本》中的勾股定理插图。勾股定理指出,黑色和红色正方形的面积之和等于下方黄色和蓝色正方形的面积。
正如亚历山大·博戈莫尔尼在他的网站 Cut the Knot 上写道,一些与平行公设等价的陈述似乎是显而易见的,而另一些则完全不然:“无论如何,勾股定理远非显而易见。令人惊奇的是,平行公设与诸如[存在一对相似但不全等的三角形]和[三角形的面积没有上限]等直观陈述等价,并且也与勾股定理等价。”
由于几个世纪以来,数学家们未能使用其他公设和公理证明平行公设,我设想他们一直在努力,试图弄清楚如果他们假设平行公设为假会发生什么。他们不断努力,但他们永远无法明确地找到矛盾之处。当他们不断努力时,他们发现了这些陈述以及许多其他与平行公设等价的陈述。如果您假设其中任何一个,您最终都会得到欧几里得几何,但如果没有它们,您可以找到通往非欧几里得几何的奇妙土地的道路,在那里,角决定长度,并且没有正方形!