本文发表于《大众科学》的前博客网络,反映了作者的观点,不一定反映《大众科学》的观点
我上周进行了第一次期中考试。我正在为数学专业的学生教授一门大致初级课程,这是他们第一批主要侧重于证明而不是计算或算法的课程之一。它比他们到目前为止上的大多数数学课都更抽象。我喜欢教这门课,因为像这样的课程让我对数学感到兴奋,所以它让我想起了我生命中的一段特殊时光。
我的期中考试中的一个问题是:描述一个R2中的集合,它既不开也不闭。
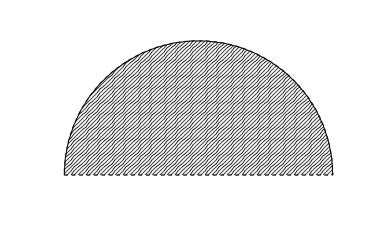
一个既不开也不闭的集合。半圆顶部的实线弧表示边界的一部分包含在该集合中,而底部的虚线表示边界的一部分不包含在该集合中。通过适当的标记和缩放,此集合可以描述为所有点 (x,y) 的集合,这些点距离点 (0,0) 小于或等于 1 个单位,并且 y 坐标严格大于 0。来源:伊芙琳·兰姆。
关于支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
“开”和“闭”当然是术语。在我们的课堂上,如果集合中的每个点周围都有一个小球也完全包含在该集合中,则该集合称为“开”。如果我们只看实数轴,区间 (0,1)——所有严格大于 0 且严格小于 1 的数字的集合——是一个开集。如果您在区间 (0,1) 中选择一个数字,无论它多么接近端点之一,它周围总有一个较小的区间也完全包含在区间 (0,1) 中。例如,数字 1/100 非常接近 0,但区间 (1/200, 1/50) 包含点 1/100 并且完全包含在区间 (0,1) 中。另一方面,区间 [0,1]——所有大于或等于 0 且小于或等于 1 的数字的集合——不是开集。[0,1] 和 (0,1) 之间的唯一区别是我们是否包含端点,但这两个小点却造成了很大的区别。点 0 周围的每个区间都包含负数,因此点 0 周围没有完全在区间 [0,1] 中的小区间。因此,区间 [0,1] 不满足开集的定义。(有关开集的更多信息,请查看维基百科或MathWorld。)
如果一个集合的补集是开集,则该集合称为“闭集”。我们的课程几乎完全在正常的欧几里得空间中进行,而不是在一些更奇特的空间中。在 d 维欧几里得空间 Rd 中,集合 A 的补集是 Rd 中但不在 A 中的所有内容。区间 [0,1] 是闭集,因为它的补集,即严格小于 0 或严格大于 1 的实数集合,是开集。
所以我的期中考试题要求学生找到一个既不开且补集也不开的集合。我以为这将是考试中最容易的问题之一,所以我很惊讶我的许多学生在这个问题上犯了同样的错误。他们没有给我既不开也不闭的集合,而是给了我既开又闭的集合!
我低估了英语语言的力量,它会向我的学生暗示数学上不正确的陈述。在数学中,“开”和“闭”不是反义词。集合可以是开集、闭集、既开又闭,或者既不开也不闭。(既开又闭的集合有时称为“开闭集”。)“闭”的定义包含一定程度的“相反性”,因为集合的补集有点像它的“相反”,但闭集和开集本身并不是相反的。如果一个集合不是开集,那并不会使其成为闭集,如果一个集合是闭集,那并不意味着它不能是开集。它们是相关的,但这不是互斥关系。但在英语中,这两个词基本上是反义词(尽管对于门和盖子,除了开和闭之外,我们还可以选择“半开半闭”)。我的学生使用了他们对英语中“开”和“闭”这两个词如何相互关联的直觉,并将这种直觉应用于这些术语的数学用法。
他们中的一些人甚至通过说“因为 [A] 是开集,所以它不是闭集,并且因为它不是闭集,所以它不是开集”之类的话来为他们的答案辩解。他们事实上知道存在一个既开又闭的集合,但他们并没有完全理解它,所以他们不知何故得出了一个自相矛盾的结论,即既开又闭的集合既不开也不闭!
当然,除了语言之外,还有其他因素在起作用:时间可能是考试环境中的一个问题,考试的压力有时会让人写出甚至他们自己后来都不明白的奇怪的东西。但我认为“开”和“闭”这两个词的数学含义和英语含义之间的差异在我的学生解答考试题时遇到了困难,这起到了很大的作用。我不认为他们会在披萨配料方面犯同样的错误。这个披萨上既有奶酪又有意大利辣香肠。奶酪不是意大利辣香肠,意大利辣香肠也不是奶酪,所以这个披萨上有“非奶酪”和“非意大利辣香肠”,因此它既没有奶酪也没有意大利辣香肠。“意大利辣香肠”和“奶酪”在英语中不是像“闭”和“开”那样的反义词。
我的学生在这个问题上的错误对我来说很有价值,我希望对他们也是如此,尽管丢了分。我了解到我的学生仍在习惯“开”和“闭”的概念,这在课程的其余部分以及更重要的是他们仍在习惯使用数学定义方面将继续很重要。我认为数学家异常擅长接受新定义,忽略先前的知识,并仅使用该定义进行工作。我们探究定义的不同部分,并尝试了解如果我们删除或添加条款,它会有什么不同。我们可以从定义中“自然而然地”获得哪些定理?正如Cathy O'Neil 在这里讨论的那样,创建好的定义是一门艺术,这在数学中非常重要。但我的学生是刚入门的数学家,他们尚未熟练掌握这门艺术。
有一个名为Math Mistakes的博客,它收集了中小学生不正确的作业的有趣例子并对其进行分析。学生犯这些错误时在想什么?解决他们的误解的最佳方法是什么?与普遍的看法相反,考试并非纯粹是折磨人的工具或惩罚的手段。考试也可以是评估学生进步和诊断学生误解的一种方式。我希望现在我已经诊断出我的课堂中对“开”和“闭”的常见误解,我可以澄清它并尝试避免将来出现类似的错误。